Next: The boundary conditions.
Up: The Laplace equation.
Previous: The Laplace equation.
We will assume that the conductive properties of the plate are
independent of direction, location, and temperature. Then
the PDE governing the temperature distribution T(x,y)
in the interior of the plate is the Laplace equation,
| 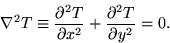 |
(15) |
It is the standard example of an elliptic equation. The Laplace
equation also governs incompressible potential flows, electrostatics,
shapes of stretched membranes, minimal surfaces, differentiable
complex functions, and many other areas.
Next: The boundary conditions.
Up: The Laplace equation.
Previous: The Laplace equation.