


Up: Return
EGN 5456 Computational Mechanics 10/30/98
Closed book Van Dommelen 8:35-9:25 am
Show all reasoning and intermediate results leading to your answer.
The following PDE describes convection of entropy in a pipe:
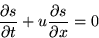
where s=s(x,t) is entropy, t time, u>0 a given constant flow
velocity in the pipe, and x the distance along the pipe.
The boundary and initial conditions are:

The length of the pipe is 2.
We want to solve this problem numerically using the following scheme:
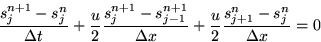
where sjn is the value of the entropy at mesh point number j
and time step number n, 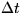 the time increment, and
the time increment, and 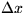 the spacing between mesh points.
the spacing between mesh points.
Discuss this scheme in as much detail as possible, discussing the
following questions fully (in any order):
- 1.
- Does the scheme make sense? (25%)
- 2.
- Will the scheme work? (25%)
- 3.
- How well will the scheme work? (25%)
- 4.
- Exactly how would you need to perform the computation? (25%)
To save time, in case you feel the need to do any Taylor series
expansions, you may represent terms involving third order derivatives
and higher by order symbols.
Solution page 1
Solution page 2
Solution page 3
'Author: Leon van Dommelen'
![]()
![]()
![]()