


Up: Return
EGN 5456 Computational Mechanics 10/27/97
Open book Van Dommelen 1:05-2:20pm
Show all reasoning and intermediate results leading to your answer.
- 1.
- Consider steady heat conduction in a plate with the
elliptical boundary x2 + y2/4 = 1. The temperature
on the elliptical boundary is T=x. Draw the isotherms
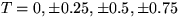 inside the plate.
Now assume that we increase the boundary temperature
on the right side of the boundary, to T=1+x, and reduce
it on the left side of the boundary, to T=-1+x.
Sketch the isotherms
inside the plate.
Now assume that we increase the boundary temperature
on the right side of the boundary, to T=1+x, and reduce
it on the left side of the boundary, to T=-1+x.
Sketch the isotherms 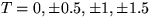 inside the plate.
inside the plate.
- 2.
- Consider entropy convection inside a pipe bend into a closed
ring of unit radius. The nonconducting inviscid entropy equation is
st + u sx = 0. Assume u is a constant velocity. Show that a
solution to this problem is
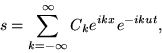
where 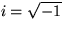 . What determines the constants Ck?
Why is this form of solution with complex exponentials
eikx more convenient than the real form
. What determines the constants Ck?
Why is this form of solution with complex exponentials
eikx more convenient than the real form
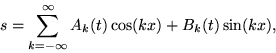
aside from the fact that there are now two different types of terms?
- 3.
- The one-dimensional inviscid momentum equation for flow
in a pipe is
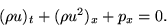
From this equation, derive a conservation law for an
arbitrary piece of pipe with moving end points. From it,
show that you can get the momentum equation in the
way expressed in your physics classes.
- 4.
- Consider one-dimensional inviscid nonconducting
isentropic flow in a pipe. The governing equations
can be expressed in terms of the flow velocity
 ,the speed of sound
,the speed of sound  , and the ratio of specific heats
, and the ratio of specific heats
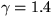 as:
as:
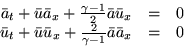
To simplify, we will linearize this to
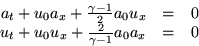
where u0 and a0 are now constant reference values of the
velocity and speed of sound, and u and a are the perturbation
velocity and speed of sound to be found. Classify this system of
equations for u and a. Find the Riemannian invariants and solve
if the initial velocity 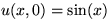 and the speed of
sound a(x,0)=0.
and the speed of
sound a(x,0)=0.



Up: Return
'Author: Leon van Dommelen'
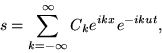
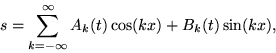
![]()
![]()
![]()
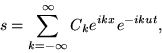
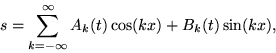
![]()
![]()
![]()