Up: Return

EGN 5456 Intro to Computational Mechanics 10/21/96
Closed book Van Dommelen 12:55-2:10 pm

Show all reasoning and intermediate results leading to your answer. One book of mathematical tables, such as Schaum's Mathematical Handbook, may be used.

1. The velocity potential for compressible unsteady potential flow in a pipe satisfies

   

   Classify this equation. According to the classification, what sort of additional conditions would you need to solve this? For example, would it be appropriate to specify only the velocity potential at a starting time? Or the velocity potential at both a starting and an ending time? Would you expect singularities in the solution at say the starting time to smooth out for later times?

2. The weak formulation for an hypothetical conservation law equation is:

   

   for all infinitely smooth that vanish outside a bounded region. Show that the following function u(x,t) is a weak solution:

   

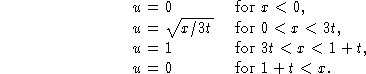
   Is the entropy condition satisfied, i.e. do the characteristics run into the shock?

3. For a certain uniform compressible flow in a pipe, small perturbations p(x,t) in the uniform pressure, u(x,t) in the uniform velocity, and s(x,t) in the uniform entropy satisfy:

   

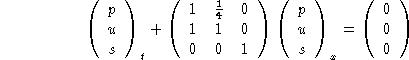
   Find the perturbations for all times, assuming that the initial conditions are:

   

   Next suppose that we would have had a finite domain , how many boundary conditions would we have needed at x=0? And how many at x=1?