EML 4930/5061 Analysis in M.E. II 03/02/11
Closed book Van Dommelen 9:35-10:25 am
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator and one
handwritten letter-size single formula sheet.
- A curve is described by
Find the unit vector in the direction of the curve, the curvature,
the normal to the curve, the binormal, and the torsion. Why are you
not surprised by the value of the torsion? Note, you should find
that the normal is
Solution.
- Suppose that an electric field has the form
Find the flux of this vector field through the spherical surface
of radius 2 centered around the point (1,1,1).
Solution.
- Transform the partial differential equation
into the wave equation with unit wave velocity by rotating and
stretching coordinates. Give the new coordinates in terms of 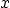 ,
,
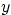 , and
, and 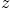 .
.
Solution.