EML 4930/5061 Analysis in M.E. II 04/26/11
Closed book Van Dommelen 3-5 pm
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator and one
handwritten letter-size single formula sheet.
- (20%) Solve the following PDE and boundary condition
Clean up your answer!
Draw the characteristics very neatly. Using your picture, answer
the following questions:
- Are there any points where the solution is not defined by the
given boundary condition? If so, identify them. What happens to
the solution that you found, if evaluated in this region?
- A boundary condition cannot in general be specified at
all
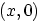 . Identify at what
. Identify at what 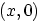 the boundary condition can
be specified to ensure a properly posed problem. (Exclude the
points mentioned in (a) from the domain. Otherwise it is
automatically improperly posed.)
the boundary condition can
be specified to ensure a properly posed problem. (Exclude the
points mentioned in (a) from the domain. Otherwise it is
automatically improperly posed.)
- Is it OK to specify the given cosine initial condition at all
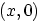 anyway? Explain.
anyway? Explain.
Solution.
- (20%) Use D’Alembert to find the deflection
 of
a vibrating string of length
of
a vibrating string of length 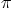 satisfying
satisfying
if the initial conditions are
Evaluate the solution at 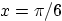 and
and 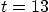 . Make sure to
explicitly list the value of each term in the expression for
. Make sure to
explicitly list the value of each term in the expression for  .
Exact value only.
.
Exact value only.
Solution.
- (20%) Use the Laplace transform method to solve the following
problem. At time zero, a plate is moving upwards with a given
velocity
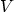 . Next to the plate is a viscous fluid that is at rest.
For times greater than zero, the plate drags along more and more
fluid next to it. The plate slows down accordingly. The motion of
the viscous fluid is described by
. Next to the plate is a viscous fluid that is at rest.
For times greater than zero, the plate drags along more and more
fluid next to it. The plate slows down accordingly. The motion of
the viscous fluid is described by
The initial condition is
(The single point where 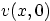 is not zero can be ignored in
transforming the PDE, but not necessarily in other manipulations.)
The boundary condition is
is not zero can be ignored in
transforming the PDE, but not necessarily in other manipulations.)
The boundary condition is
where  is a constant, related to the fluid viscosity and plate
mass per unit area, with units of velocity. Solve this problem,
assuming that
is a constant, related to the fluid viscosity and plate
mass per unit area, with units of velocity. Solve this problem,
assuming that 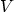 ,
, 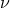 , and
, and  are given constants. Note: the
back transform is not in tables 6.3 or 6.4 and probably messy to
derive. You can find it in Schaum’s Mathematical Handbook, for
one. Clean up.
are given constants. Note: the
back transform is not in tables 6.3 or 6.4 and probably messy to
derive. You can find it in Schaum’s Mathematical Handbook, for
one. Clean up.
Use only the Laplace transform tables 6.3 and 6.4 except where
stated otherwise.
Solution.
- (40%) Use separation of variables to solve the following
problem for viscous flow in between two plates in which one plate exerts
a quadratically increasing shear force on the fluid:
Show all reasoning. List the eigenfunctions and eigenvalues
completely.
At the end, write out the fully worked out solution completely, with
all parameters in it clearly identified.
Solution.
Table 6.3: Properties of the Laplace Transform
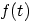 |
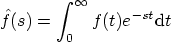 |
1.
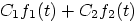 |
 |
2.
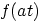 |
 |
3.
 |
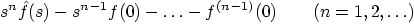 |
4.
 |
 |
5.
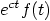 |
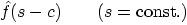 |
6.
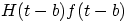 , where , where |
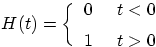 |
|
 |
7.
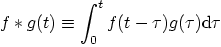 |
 |
Table 6.4: Laplace Transform Pairs
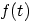 |
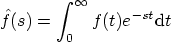 |
1.
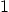 |
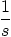 |
2.
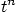 |
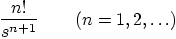 |
3.
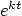 |
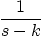 |
4.
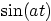 |
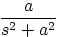 |
5.
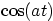 |
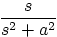 |
6.
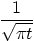 |
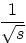 |
7.
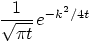 |
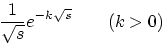 |
8.
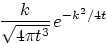 |
 |
9.
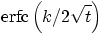 ,
where ,
where |
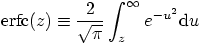 |
|
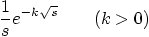 |