EML 4930/5061 Analysis in M.E. II 03/03/10
Closed book Van Dommelen 9:40-10:30 am
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator and one
handwritten letter-size single formula sheet.
- Consider the vector field
Find the curl of this vector field. Show that 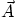 must be the
gradient of some function
must be the
gradient of some function 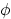 . Then rigorously derive the most
general form of this function. Now consider the line integral
. Then rigorously derive the most
general form of this function. Now consider the line integral
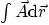 starting from the origin to the point (1,1,1)
through the path
starting from the origin to the point (1,1,1)
through the path
and then back again to the origin over the path
Give the value of this integral. Also give the value of the two
individual pieces that the integral consists of.
Solution.
- Consider the curvilinear coordinates
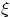 ,
, 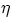 , and
, and 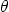 given by
given by
Show that this curvilinear coordinate system is orthogonal. Find
the metric indices 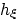 ,
, 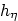 , and
, and  . Using these
metric indices only, find the derivative of the unit vector
. Using these
metric indices only, find the derivative of the unit vector
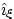 with respect to
with respect to 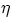 .
.
Solution.
- Classify and solve the PDE
Suppose you wanted to solve this PDE in a rectangle in the
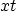 -plane, what would be appropriate BC/IC to add?
-plane, what would be appropriate BC/IC to add?
Solution.