EML 4930/5061 Analysis in M.E. II 04/27/10
Closed book Van Dommelen 3-5 pm
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator and one
handwritten letter-size single formula sheet.
- (20%) Solve the following PDE and boundary condition
Draw at least four characteristics very neatly in the 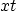 -plane.
Explain why there is no boundary condition at
-plane.
Explain why there is no boundary condition at 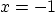 . Explain why
there is no initial condition given.
. Explain why
there is no initial condition given.
Solution.
- (20%) Use D’Alembert to find the pressure
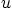 to the
problem of acoustics in a pipe of length
to the
problem of acoustics in a pipe of length 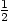 with one end
closed,
with one end
closed,
if the initial conditions are
Use your results to evaluate 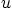 at
at 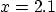 and
and 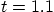 if
if 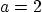 .
Exact value only.
.
Exact value only.
Solution.
- (40%) Solve the following wave propagation problem of
acoustics in a pipe that is forced at its ends:
Show all reasoning. List the eigenfunctions and eigenvalues
completely. Write out the fully worked-out solution precisely and
completely. Hint: for brevity, write 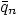 as
as 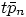 .
.
Solution.
Solution.
- (20%) Solve the following problem of supersonic flow
along a wavy plate using the Laplace transform method:
where 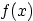 is to be considered to be some given function and
is to be considered to be some given function and
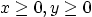 . Show all steps and reasoning. Your answer should
not have weird mathematics, but be in simple terms that anyone with
a basic understanding of calculus can understand. Use convolution
only if it is unavoidable. If
. Show all steps and reasoning. Your answer should
not have weird mathematics, but be in simple terms that anyone with
a basic understanding of calculus can understand. Use convolution
only if it is unavoidable. If 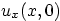 gives the pressure on the
surface, then what is it in terms of
gives the pressure on the
surface, then what is it in terms of 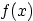 ?
?
Solution.
Table 6.3: Properties of the Laplace Transform
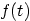 |
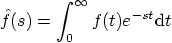 |
1.
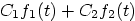 |
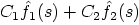 |
2.
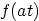 |
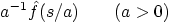 |
3.
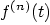 |
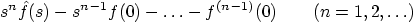 |
4.
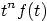 |
 |
5.
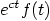 |
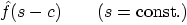 |
6.
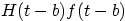 , where , where |
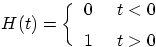 |
|
 |
7.
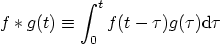 |
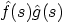 |
Table 6.4: Laplace Transform Pairs
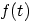 |
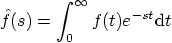 |
1.
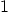 |
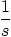 |
2.
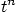 |
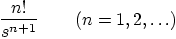 |
3.
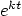 |
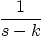 |
4.
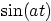 |
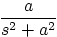 |
5.
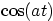 |
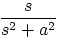 |
6.
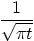 |
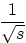 |
7.
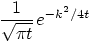 |
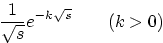 |
8.
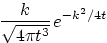 |
 |
9.
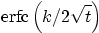 ,
where ,
where |
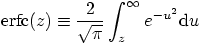 |
|
 |