EML 4930/5930 Analysis in M.E. II 03/03/08
Closed book Van Dommelen 9:40-10:30 am
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator and one
handwritten letter-size single formula sheet.
- Consider the following volume in Cartesian coordinates, shaped
like a square cylinder with an uneven top assuming that
 is
upwards:
is
upwards:
There is a heat flux through this volume given by
and we are interested in the net heat flow coming out of the volume,
as given by
where 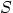 consists of all 6 outside surfaces of the volume.
consists of all 6 outside surfaces of the volume.
- Show that the heat flow out of the bottom surface
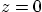 is zero.
is zero.
- Show that the heat flow out of the side surfaces
 ,
, 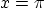 ,
,
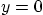 , and
, and 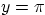 is also zero.
is also zero.
- That leaves the heat flow through the top surface. Write an
explicit expression for
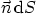 in terms of
in terms of  and
and  for
this top surface.
for
this top surface.
- Write the integral to be evaluated on the top surface out
completely, but do not integrate it yet.
- Show that
![$\vec q =\nabla\times\big[\sin(x)\sin(y)\hat k\big]$](_img14.gif) .
.
- Based on that fact, explain what the top integral will be.
Solution.
- Boundary layer coordinates
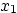 ,
, 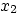 , and
, and 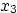 are defined
by the following expression for the position vector
are defined
by the following expression for the position vector
 :
:
where 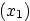 indicates that those vectors are functions of
indicates that those vectors are functions of 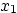 .
In particular,
.
In particular,
and 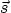 ,
, 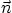 and
and 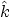 are a set of mutually orthogonal
unit vectors.
are a set of mutually orthogonal
unit vectors.
- Explain why
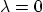 .
.
- Explain why this is an orthogonal curvilinear coordinate
system.
- Find the expression for the Laplacian of a quantity
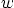 in
terms of these coordinates.
in
terms of these coordinates.
- Work the expression out completely.
Solution.
- Consider the following partial differential equation
- Find a particular solution.
- Classify the equation.
- Derive the general solution
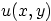 to the equation,
(expressed in terms of
to the equation,
(expressed in terms of  and
and  , of course).
, of course).
Solution.