EML 4930/5930 Analysis in M.E. II 02/21/07
Closed book Van Dommelen 9:40-10:30 am
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator and one
handwritten letter-size single formula sheet.
- Consider the following curve given in terms of a parameter
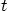 :
:
Find the unit tangential vector to the curve in terms of 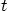 and find its
curvature. Also, if
and find its
curvature. Also, if 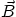 is the unit vector normal to the
osculating plane of the curve, find the direction of the rate
of change of
is the unit vector normal to the
osculating plane of the curve, find the direction of the rate
of change of 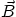 with respect to the arclength along the curve.
with respect to the arclength along the curve.
Solution.
- Consider the following force field:
Find the most general possible form of function 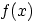 for which this force field is conservative. Derive the most
general expression for the potential energy, fully specifying
all dependencies.
for which this force field is conservative. Derive the most
general expression for the potential energy, fully specifying
all dependencies.
Solution.
- Boundary layer coordinates
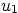 ,
, 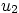 , and
, and 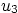 are defined
by the following expression for the position vector
are defined
by the following expression for the position vector
 :
:
Here 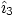 is a constant vector, but
is a constant vector, but 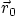 and
and 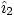 depend on
depend on 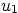 . In particular,
. In particular,
where 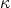 is a function of
is a function of 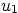 .
The vectors
.
The vectors  ,
, 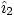 and
and 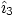 are orthogonal
unit vectors.
are orthogonal
unit vectors.
- Show that boundary layer coordinates are orthogonal curvilinear
coordinates.
- Derive the scale factors or metric indices.
- Derive the derivatives of the unit vectors with respect to the
coordinate directions. Note the given data, such as that
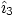 is a constant vector.
is a constant vector.
Solution.