EML 4930/5930 Analysis in M.E. II 02/22/06
Closed book Van Dommelen 9:15-10:05 am
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator and one
handwritten letter-size single formula sheet.
- A daredevil on a motorcycle is spiraling along the inner surface
of a large diameter horizontal pipe. The path of his center of
gravity is given by
with the  -axis vertically upwards. Find the radius of curvature
of his path in terms of
-axis vertically upwards. Find the radius of curvature
of his path in terms of 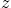 ; also find the unit vector normal to his path.
; also find the unit vector normal to his path.
Now assume that his kinetic energy is given by
where  is his speed at the bottom of the pipe. How slow can he
go on the bottom before he falls off the top of the pipe?
is his speed at the bottom of the pipe. How slow can he
go on the bottom before he falls off the top of the pipe?
Solution.
- A velocity field is given by
Find the volumetric flow rate
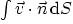 through
the octant of a spheroid given by
through
the octant of a spheroid given by
(Hint: To simplify the final integral, define a new coordinate 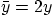 .)
.)
Solution.
- The neutron density
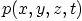 in a radioactive material is
the number of neutrons in the material per unit volume. Assume that
each volume element
in a radioactive material is
the number of neutrons in the material per unit volume. Assume that
each volume element 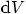 produces additional neutrons
produces additional neutrons 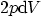 per unit time.
per unit time.
The production of additional neutrons in a volume will equal the
rate of increase of the number of neutrons in the considered volume
plus the neutrons escaping through the surface of the solid. If the
net number of neutrons leaving through the surface of any volume of
the material is
with 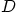 some diffusion constant, write an integral law for the rate
of change of neutrons in an arbitrary volume in terms of the
production and the neutrons leaving through its surface. From this,
find a partial differential equation for the evolution of the
neutron density with time.
some diffusion constant, write an integral law for the rate
of change of neutrons in an arbitrary volume in terms of the
production and the neutrons leaving through its surface. From this,
find a partial differential equation for the evolution of the
neutron density with time.
Solution.