Up: Return
EML 5060 Analysis in Mechanical Engineering 12/14/99
Closed book Van Dommelen 5:30-7:30 pm
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator and a single
A4-size handwritten formula sheet.
- 1.
- Solve unsteady viscous flow in a duct of constant width.
The coordinate across the duct is x, so that after normalizing
the duct width to unity,
 . The flow velocity
through the duct, u(x,t), is governed by the Navier-Stokes P.D.E.
. The flow velocity
through the duct, u(x,t), is governed by the Navier-Stokes P.D.E.
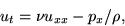
where we can normalize things so that the coefficient of viscosity
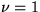 and the pressure gradient
and the pressure gradient 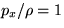 too. Assume the motion
starts from rest, u(x,0)=0, and that the fluid is at rest at the
walls of the duct, u(0,t)=u(1,t)=0. Solve for u(x,t) by
formulating an eigenfunction expansion for u and then deriving and
solving ordinary differential equations for the coefficients. (In
other words, do not define another variable instead of u, by,
say, substracting a steady solution, as you might have seen done in
some books.)
Solution.
too. Assume the motion
starts from rest, u(x,0)=0, and that the fluid is at rest at the
walls of the duct, u(0,t)=u(1,t)=0. Solve for u(x,t) by
formulating an eigenfunction expansion for u and then deriving and
solving ordinary differential equations for the coefficients. (In
other words, do not define another variable instead of u, by,
say, substracting a steady solution, as you might have seen done in
some books.)
Solution.
- 2.
- The temperature at the end of a semi-infinite bar is suddenly a
bit increased. The resulting small temperature increase u(x,t)
satisfies the heat equation with an additional radiation term:
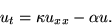
At time zero, the incremental temperature is still zero away from the
end, u(x,0)=0 for x>0. The boundary condition at the end of the
bar is  , where
, where 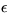 is a constant. Solve for
u(x,t). Hint: it may actually be simpler first to solve for a
general boundary condition u(0,t)=f(t) and then put in the given
value for f at the last moment.
Solution.
is a constant. Solve for
u(x,t). Hint: it may actually be simpler first to solve for a
general boundary condition u(0,t)=f(t) and then put in the given
value for f at the last moment.
Solution.
- 3.
- The initial transverse displacement u(x,t) of a guitar string
of length 2 is given by:
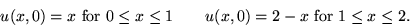
and the initial transverse velocity is zero. Find the transverse
displacement in the middle of the string at time t=19 if the wave
propagation speed in the string a=0.25.
Solution.
- 4.
- Solve the unsteady vibrations of the membrane on a circular drum.
The membrane displacement
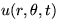 satisfies the wave equation
satisfies the wave equation
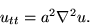
The boundary condition at the edge is
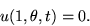
For initial condition, assume that the membrane is struck at
the point r=0.5 and 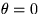 . In other words assume that
. In other words assume that
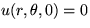 and that
and that 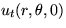 is a delta
function at r=0.5 and
is a delta
function at r=0.5 and 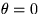 , so that
, so that

for any function 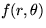 .Solution.
.Solution.
Up: Return
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()