


Up: Return
EML 5060 Analysis in Mechanical Engineering 12/11/98
Closed book Van Dommelen 10:00-12:00am
Show all reasoning and intermediate results leading to your answer.
One book of mathematical tables, such as Schaum's Mathematical Handbook,
may be used, as well as a standard size handwritten formula sheet.
- 1.
- (25%)
Classify the following Partial Differential Equation:
uxx + 4 uxy + 3 uyy = 0
Put it in characteristic coordinates and solve it. Rewrite the
solution in terms of the original coordinates x and y.
Solution.
- 2.
- (25%)
A pipe that is closed at both ends contains air. Initially the air
and pipe are at rest. Then, at time zero, the pipe is impulsively
given a unit velocity along its axis. Find the velocity u(x,t) of
the air in the pipe. From fluid mechanics, it may be derived that
this velocity satisfies the following Partial Differential Equation:
utt = a2 uxx,
where a is a known constant (the speed of sound.)
For this problem, the initial and boundary conditions are:
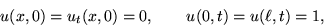
where 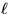 is the length of the pipe. Give a set of suitable
functions to expand the solution u(x,t) in. Then give the solution
u(x,t) in terms of these functions.
Solution part 1.
Solution part 2.
is the length of the pipe. Give a set of suitable
functions to expand the solution u(x,t) in. Then give the solution
u(x,t) in terms of these functions.
Solution part 1.
Solution part 2.
- 3.
- (25%)
One end of a very long bar is suddenly, at time zero, raised
to a unit temperature. The further evolution of the temperature
distribution u(x,t) in the bar is described by the following
Partial Differential Equation:
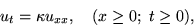
where 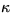 is the conduction coefficient. The initial and
boundary conditions are:
is the conduction coefficient. The initial and
boundary conditions are:

Find the solution u(x,t) using a Laplace transform. From it, show that
the temperature is constant on points that move away from the end
as x = (constant) 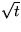 .Solution.
.Solution.
- 4.
- (25%)
Solve the unsteady vibrations of the membrane on a circular drum.
The membrane displacement
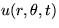 satisfies the wave equation
satisfies the wave equation
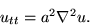
The boundary condition at the edge is
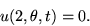
For initial condition, assume that the membrane is struck at
the point r=1 and 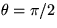 . In other words assume that
. In other words assume that
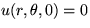 and that
and that  is a delta
function at r=1 and
is a delta
function at r=1 and 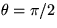 . This means that
. This means that
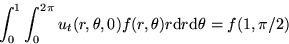
for any function 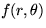 .
What frequencies will be present in the vibrations, and with
what relative strength?
Solution.
.
What frequencies will be present in the vibrations, and with
what relative strength?
Solution.



Up: Return
'Author: Leon van Dommelen'
![]()
![]()
![]()
![]()
![]()
![]()