Up: Return
EML 5060 Analysis in Mechanical Engineering 12/9/97
Closed book Van Dommelen 5:30-7:30 pm
Show all reasoning and intermediate results leading to your answer.
One book of mathematical tables, such as Schaum's Mathematical Handbook,
may be used.
- 1.
- The Laplace equation describes many important physical processes such
as steady heat conduction, potential flows, electrostatic fields,
etcetera. In order to solve the Laplace equation in two dimensions
numerically, we might try to add an artificial time coordinate.
Suppose we create the equation
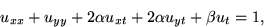
where 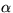 and
and 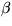 are constants. What is the classification
of this equation for various
are constants. What is the classification
of this equation for various 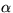 and
and 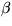 ?
Solution
?
Solution
- 2.
- Consider unsteady heat conduction in a bar of length
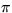 . Assume
that the heat conduction coefficient
. Assume
that the heat conduction coefficient 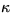 is unity. Assume that
the bar is initially at temperature zero, u(x,0)=0, but there is a
heat flux out of the bar at the left end, ux(0,t)=t and the same heat
flux into the bar at the right end,
is unity. Assume that
the bar is initially at temperature zero, u(x,0)=0, but there is a
heat flux out of the bar at the left end, ux(0,t)=t and the same heat
flux into the bar at the right end, 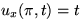 . Find the
temperature u(x,t) for arbitrary time. From the result, determine
how the temperature profile in the bar looks for large times.
Solution
. Find the
temperature u(x,t) for arbitrary time. From the result, determine
how the temperature profile in the bar looks for large times.
Solution
- 3.
- For the bar of the previous question, let us try to figure out
how the temperature u(x,t) looks near the left end of the bar for
very small times. To do so, we can ignore the effect of the right
end. In other words, we will now take the bar to be semi-infinite.
Solve this problem. From the solution, determine roughly how far the
bar near the left end will be cooled for small times t.
Solution
- 4.
- The membrane of a circular drum is hit with a drum stick at a point
halfway between the center of the drum and the rim. After scaling,
the vibrations of the drum are governed by
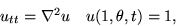
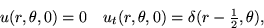
where
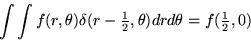
for any function f.
Solution
Up: Return
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()