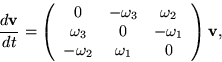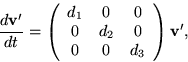Up: Return
EML 5060 Analysis in Mechanical Engineering 10/18/96
Closed book Van Dommelen 9:00-9:50am
Show all reasoning and intermediate results leading to your answer.
One book of mathematical tables, such as Schaum's Mathematical Handbook,
may be used.
- 1.
- In the numerical solution of the simplest one-dimensional
heat conduction problem, you need to solve a linear system
of equations with a `tridiagonal' matrix of the form:
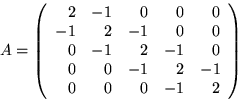
The work in solving this five by five system
is not as much as you would expect due to all those zeros.
They remain zeros.
Show that this is true by solving 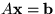 if
if 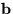 is the
unit vector
is the
unit vector
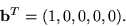
Use Gaussian elimination without partial pivoting. The inverse matrix
A-1 is bad news since it does not have all these zeros. (The
solution vector 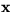 is the first column of A-1).
Solution
is the first column of A-1).
Solution
- 2.
- The two spring-mass systems below have identical masses m=1 and
spring constants k1. Unfortunately, they resonate since there is
an external disturbance of frequency
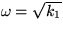 present. In the
hope of eliminating the resonance, you provide some mutual support
to the masses by attaching a second spring with stiffness k2 between
them. The new equations of motion are:
present. In the
hope of eliminating the resonance, you provide some mutual support
to the masses by attaching a second spring with stiffness k2 between
them. The new equations of motion are:

Substitute in the assumptions
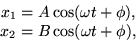
where A, B, and  are constants, to get an eigenvalue problem for
the frequency
are constants, to get an eigenvalue problem for
the frequency 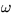 . Answer the question whether the
additional spring eliminates the resonating frequency. If not, give
the physical reason why not.
. Answer the question whether the
additional spring eliminates the resonating frequency. If not, give
the physical reason why not.
(lost picture showing from left to right: wall, spring k1, mass m,
spring k2, mass m, spring k1, wall)
Solution
- 3.
- In a slowly rotating coordinate system,
the relative velocity vector
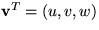 of a mass
satisfies the equations of motion
of a mass
satisfies the equations of motion
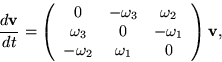
assuming that no forces act on the mass.
Diagonalize the matrix and then solve the above differential equations
for the diagonal matrix, in other words, solve
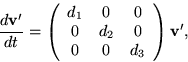
Show that the solution is periodic in time.
Explain why you are not (or should not be) surprised for physical reasons.
Solution
Up: Return
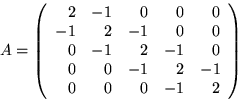
![]()
![]()
![]()
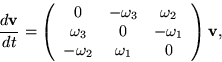
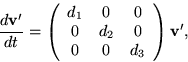
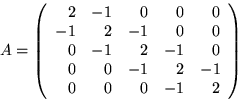
![]()
![]()
![]()