Up: Return
EML 5060 Analysis in Mechanical Engineering 12/12/96
Closed book Van Dommelen 10:00-12:00am
Show all reasoning and intermediate results leading to your answer.
One book of mathematical tables, such as Schaum's Mathematical Handbook,
may be used.
- 1.
- (30 points)
In the separation-of-variables solution of a heat conduction problem
with a mixed and a Dirichlet boundary condition, you encounter the
following Sturm-Liouville problem:
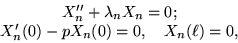
with p a positive constant.
Show that there are no nontrivial solutions to this Sturm-Liouville
problem for negative or zero 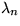 . Find an approximation for
the values of the large eigenvalues
. Find an approximation for
the values of the large eigenvalues 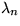 . Solution
. Solution
- 2.
- (30 points)
Solve the following wave propagation problem:
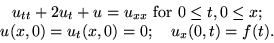
Solution
- 3.
- (40 points)
Find the steady temperature
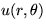 in a circular plate of
radius one if the normalized heat flow out of the edge of the
plate
in a circular plate of
radius one if the normalized heat flow out of the edge of the
plate 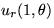 is a given function
is a given function 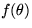 .Use separation of variables.
List the Sturm-Liouville problem that gives rise to the
eigenfunctions, and list the complete set of resulting eigenfunctions.
Show that function
.Use separation of variables.
List the Sturm-Liouville problem that gives rise to the
eigenfunctions, and list the complete set of resulting eigenfunctions.
Show that function 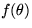 must satisfy a constraint
in order for a solution to exist. What is the physical reason
for the constraint?
Also show that the solution can be written in the form
must satisfy a constraint
in order for a solution to exist. What is the physical reason
for the constraint?
Also show that the solution can be written in the form
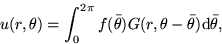
for some function 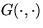 . Solution
. Solution
Up: Return
![]()
![]()
![]()
![]()
![]()
![]()