Up: Return
EML 5060 Analysis in Mechanical Engineering 9/22/95
Closed book Van Dommelen 9:00-9:50 EST
Show all reasoning and intermediate results leading to your answer.
One book of mathematical tables, such as Schaum's Mathematical Handbook,
may be used.
- 1.
- (33 points).
Six points P1, P2, P3, P4, P5, and P6
in a certain structure have to be grounded. The person in charge
did not do a good job. The person connected point
P1 to P2 with an electrical wire, and the person also connected
point P2 to P3. The person connected P4 to P5,
P5 to P6, and P6 to P4. But the person did not connect
any point to the ground! In view of the points that the person connected,
we can say the following about the electric potentials
V1, V2, V3, V4, V5, and V6:
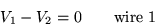

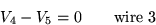

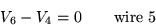
Show that the rank of this system of 5 equations in 6 unknowns
is one less than what you would expect. What does this mean in terms of
the wires that the person has used? Do the potentials have to be zero at all
six points? Do they all have to be the same?
Solution
- 2.
- (33 points).
You are designing a machine to automatically polish the surface
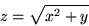
Of course, the plane of the polishing disk needs to be tangential to the
surface at all times. So what is the equation of the plane of the
polishing disk to polish the point where x=2 and y=5?
Solution
- 3.
- (34 points).
The kinetic energy of a rotating plate is given by

where 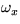 and
and 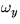 are the components of the angular velocity
vector. Suppose that it is known that T=1. What is the maximum
possible magnitude of the angular velocity vector
are the components of the angular velocity
vector. Suppose that it is known that T=1. What is the maximum
possible magnitude of the angular velocity vector 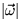 in
that case? Hint: simplify the quadratic form.
Solution
in
that case? Hint: simplify the quadratic form.
Solution
Up: Return
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()