


Up: Return
EML 5060 Analysis in Mechanical Engineering 9/19/94
Closed book Van Dommelen 9:00-9:50 EST
- 1.
- (30 points).
To keep up with the high cost of living in the party capital of the
USA, you moonlight as an artist.
To beautify a College of Engineering, you want to design an artwork
to be suspended from the ceiling.
The fee you will receive increases with the weight of the
artwork, since the bigger and more yellow, the better.
You estimate your fee to be
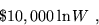
where W is the weight in pounds.
However, weights above about ten pounds involve rapidly rising
insurance costs due to the possibility of the art work breaking
loose and hitting a student or even a faculty member.
Above about 30 pounds, this cost levels off when the artwork will
essentially kill off everything in its path.
Asssume that insurance costs reduce your profit by
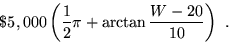
Since you will be using cheap colored plastic, material cost is
negligible, but there is a $50 labor cost you must pay.
Draw the graphs of fee and insurance cost versus weight.
Determine the weight for the artwork that maximizes your profit,
and how much you will get.
The maximum weight that can be suspended is 25 pounds.
- 2.
- (30 points).
To show that the students in Tallahasee are also capable of serious
effort, you decide to go canoe on lake Jackson.
At a given instance, the plane of your paddle is described by
x+2y+5z=20. At that moment you are drawing the paddle through the
water with speed
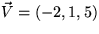 .Of course, only the component of the velocity normal to the plane
of the paddle will do you much good.
Give the unit normal to the paddle and the normal velocity component.
.Of course, only the component of the velocity normal to the plane
of the paddle will do you much good.
Give the unit normal to the paddle and the normal velocity component.
- 3.
- (40 points).
Your little excursion has tired you.
To better understand the forces you must exert, compute the moment of
inertia
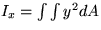 for rotation about the middle of the paddle.
Assume the straight sides of the paddle are given by x=-0.5 and
x=0.5, while the curved top and bottom satisfy x4 + y4 = 1.
The resulting integral cannot be done analytically.
Instead, expand its integrand in a series of two nonzero terms, and
integrate that.
for rotation about the middle of the paddle.
Assume the straight sides of the paddle are given by x=-0.5 and
x=0.5, while the curved top and bottom satisfy x4 + y4 = 1.
The resulting integral cannot be done analytically.
Instead, expand its integrand in a series of two nonzero terms, and
integrate that.



Up: Return
'Author: Leon van Dommelen'
![]()
![]()
![]()
![]()