


Up: Return
Exam 3 Analysis in Mechanical Engineering 11/16/93
Closed book Van Dommelen 2:45-4:00
Show all reasoning. One book of mathematical tables may be used.
- 1.
- The direction of the field lines of a two-dimensional
electrostatic field is given by:
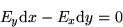
Find an algebraic expression for the field lines of the field:
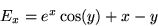
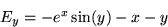
- 2.
- For the RCL circuit shown below, the voltage across the condensator
satisfies
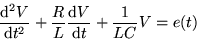
Assuming that the resistance R=3, capacitance C=0.5 and inductance
L=1, and the applied voltage is e(t)= - e-t/(1+et),
find the voltage across the condensator.
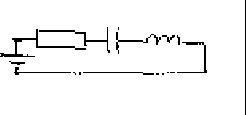
- 3.
- A projectile is fired through a constant area, but variable
density duct. Assuming the velocity variation is linear with distance,
the equation of motion for the projectile is
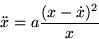
where a is a constant that cannot be scaled out.
Assuming that a=1, find an algebraic expression relating the projectile
velocity  to its position x.
Verify that the projectile never catches up with the stream:
projectile velocity does not become equal to position at large x.
to its position x.
Verify that the projectile never catches up with the stream:
projectile velocity does not become equal to position at large x.
'Author: Leon van Dommelen'
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()