


Up: Return
EML 5060 Analysis in Mechanical Engineering 9/21/93
Closed book Van Dommelen 14:45-16:00 EST
One book of mathematical tables and integrals may be used. No calculus books.
Clearly show all steps in your derivation: the method is more important than
the solution.
- 1.
- In the separation of unsteady boundary layers from the wall, certain
characteristic lines satisfy the relationship:
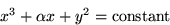
Draw these characteristics both before separation, assuming 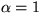 ,and beyond separation, where
,and beyond separation, where 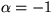 . Vary the constant to get
a picture of all lines.
. Vary the constant to get
a picture of all lines.
- 2.
- A pendulum clock operates accurately at the factory.
If this clock is shipped to a location
where gravity may differ up to 0.01m/sec2,
and the length of the
pendulum may also change by 0.1% during shipping,
what is the maximum time lost or
gained per month by the pendulum at the new location?
The frequency of vibration of a
pendulum is
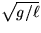 .
. - 3.
- In CAD/CAM you have created a solid which can be described as
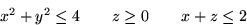
Describe the shape of the solid.
A power failure occurs before you can ask the computer to find the
center of gravity.
Fortunately the solid is of constant density, and you have no
difficulty
finding the centroid analytically. Just find the
z position of the centroid.



Up: Return
'Author: Leon van Dommelen'
![]()
![]()
![]()
![]()