


Up: Return
Final Analysis in Mechanical Engineering Due 12/15/93
Take HomeVan Dommelen
Show all reasoning.
Solutions must be neat and logically presented.
No attempt will be made to `figure it out':
what I do not understand I do not give credit for.
Any book can be used.
Asking another student, TA, or instructor a question about a particular
difficulty is allowed only if you have made all reasonable attempts to
resolve the difficulty yourself.
The question must be restricted to the minimum information needed to
get started again.
Looking at another student's solution or notes, allowing another to look at
your solution or notes, or finding a complete or significant part of a solution
together with another student or students is not allowed.
- 1.
- Solve question 7.28 using series expansion to find the natural frequencies for
the pressure in
an acoustic duct that is closed at x=0 and open at
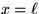 .Now approximate the pressure
at x=0 using the most important 2 non-zero terms in the expansion,
assuming that the speed of sound a=1,
.Now approximate the pressure
at x=0 using the most important 2 non-zero terms in the expansion,
assuming that the speed of sound a=1, 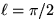 , and
that the initial pressure p(x,0)=0
while pt(x,0)=1 for x<1 and 0 for x>1.
Take the time for your approximation to be 2. followed by your
social security number.
, and
that the initial pressure p(x,0)=0
while pt(x,0)=1 for x<1 and 0 for x>1.
Take the time for your approximation to be 2. followed by your
social security number.
- 2.
- Solve the same problem exactly using D'Alembert's formula.
- 3.
- Find the vibrations of a very long string with at the end at x=0
a moving flexible support, by solving 7.36 using the Laplace transform.
From it, find the amplitude at t=1. followed by your social
security number and at x=1., assuming that a=p=1 and the motion
of the end is linear, i.e. f(t)=t. Also find the displacement at the
point given by interchanging the two values of x and t.
- 4.
- Find the steady temperature distribution in a square plate with given
heat flow into or out the four edges by solving problem 7.37.
Assume that the left and bottom sides are insulated,
p=f=0 and that there is constant heat flow through the top
and right hand sides, q=constant and g=constant,
find a two term approximation to the temperature when x=0.5 and
y=0. followed by your social security number.
The lower left corner is at zero temperature; assume q=1.
- 5.
- Solve the steady heat conduction in a unit circle with given heat flow
through the perimeter by solving problem 7.38.
Find the temperature at r=0.5 and
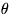 a decimal point
followed by your social security number,
if there is constant heat flow through the top half perimeter
and none through the bottom, and the center is at zero temperature.
a decimal point
followed by your social security number,
if there is constant heat flow through the top half perimeter
and none through the bottom, and the center is at zero temperature.
- 6.
- Solve unsteady heat conduction on the same unit circle, if the
boundary is insulated. The problem for
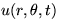 is
is
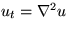
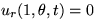 Now assume that at time t=0, the solution has already evolved
sufficiently that the only remaining term in the series expansion is
the one that decays slowest in time. In that case, how long does it take
for this solution to decay further so that only the
fraction given by a decimal point
followed by your social security number is left?
Now assume that at time t=0, the solution has already evolved
sufficiently that the only remaining term in the series expansion is
the one that decays slowest in time. In that case, how long does it take
for this solution to decay further so that only the
fraction given by a decimal point
followed by your social security number is left?



Up: Return
'Author: Leon van Dommelen'