


Up: Return
EML 5060Analysis in Mechanical Engineering Exam 111/12/92
Exam 2 Van Dommelen 2:45-4:10pm
- 1.
- (Vibrations, 19 points)
A spring mass system attached to an elastic foundation can be
written as a third order differential equation.
For a particular case, the equation
of motion is of the form
x''' + 3 x'' + 3 x' + x = 0
where primes are derivatives with respect to time.
Find the solution if initially x=0, x'=1, and x''=0.
- 2.
- (Solid mechanics, 19 points)
The elevation u of a membrane near a corner
has a radial variation with distance from the corner
given by the differential equation

where c>0 is a constant depending on the angle of the corner.
Solve for u(r).
- 3.
- (Fluid mechanics, 21 points)
When we cut a slot in a wall and apply suction through the slot,
the boundary layer profile of the air approaching the slot
satisfies according to Schlichting the ODE:
f''' - f'2 + 1 = 0
The solution satisfies  and
and 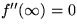 .Reduce this equation to a separable first order one. Because of time
constraints, you need not actually solve the first order equation.
.Reduce this equation to a separable first order one. Because of time
constraints, you need not actually solve the first order equation.
- 4.
- (Fluid mechanics, 21 points)
The velocity potential
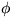 in steady
two-dimensional compressible flow satisfies
the equation
in steady
two-dimensional compressible flow satisfies
the equation
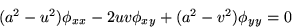
in which a is the speed of sound and
u and v are the velocity components in the x- and
y-directions, respectively. The characteristics of this equation
are called `Mach-lines' and can be seen using Schlieren
optics. Determine under which conditions Mach-lines can
occur, and give their direction.
- 5.
- (Design, 20 points)
The electrostatic field
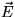 due to charged bodies
is conservative and follows from
a potential V. Each component of the field strength, as well as the
potential all satisfy the Laplace equation.
I want to suspend a positively charged particle freely in outer
space in stable
equilibrium
by surrounding it by a number of cleverly shaped charged bodies.
After 200 hours of Cray YMP processing, I still haven't found body shapes
which will give a stable suspension. The graduate students in my class
think it won't work.
But it seems obvious to me
that if I surround the particle at all sides by positively charged bodies
repulsing the particle, I am bound to trap it in the center.
Find out who is right and explain.
due to charged bodies
is conservative and follows from
a potential V. Each component of the field strength, as well as the
potential all satisfy the Laplace equation.
I want to suspend a positively charged particle freely in outer
space in stable
equilibrium
by surrounding it by a number of cleverly shaped charged bodies.
After 200 hours of Cray YMP processing, I still haven't found body shapes
which will give a stable suspension. The graduate students in my class
think it won't work.
But it seems obvious to me
that if I surround the particle at all sides by positively charged bodies
repulsing the particle, I am bound to trap it in the center.
Find out who is right and explain.



Up: Return
'Author: Leon van Dommelen'
![]()
![]()
![]()
![]()