


Up: Return
EML 5060Analysis in Mechanical Engineering Exam 1 10/1/92
Exam 1 Van Dommelen 2:45-4:10pm
- 1.
- A mass spirals outward, the distance from the center being given by
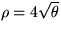 . If the rate of change in angular position
is
. If the rate of change in angular position
is 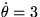 , find the radial and azimuthal components of
velocity
, find the radial and azimuthal components of
velocity 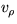 and
and 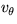 , and those of the acceleration
, and those of the acceleration
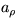 and
and 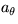 .
. - 2.
- Find the moment of inertia
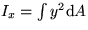 for the inside
of the polar curve
for the inside
of the polar curve

Note: for even integer p
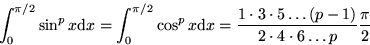
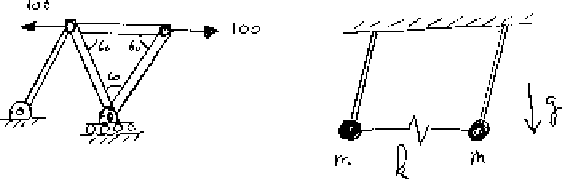
- 3.
- For the truss sketched below, the tension forces T1, T2, T3,
and T4 in the four bars satisfy the five equations:
T1 + T2 = 0
-T1 + T2 + 2 T4 = 200
T2 - T3 = 0
- T3 = 2 P
T3 + 2 T4 = 200
Write the augmented matrix of the system and determine for which value(s)
of P a solution exists, and whether it is unique.
- 4.
- A coupled set of pendula as shown above has modes of the form

For certain values of the spring constant, masses, and pendulum lengths,
the amplitudes satisfy

Find the natural frequencies 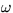 .For each frequency, compare
.For each frequency, compare 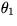 and
and 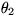 .
. - 5.
- The kinetic energy of a certain thin plate due to rotation around
its center of gravity has the form
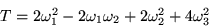
In principal axes, there would be no 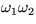 term.
Find the direction of the principal axes of this body by diagonalizing
the quadratic form.
term.
Find the direction of the principal axes of this body by diagonalizing
the quadratic form.



Up: Return
'Author: Leon van Dommelen'
![]()
![]()

![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()