


Up: Return
EML 5060 Analysis in Mechanical Engineering 4/23/92
Closed book Van Dommelen 12:30-2:30pm
Show all reasoning and intermediate results leading to your answer.
One book of mathematical tables, such as Schaum's Mathematical Handbook,
may be used.
- 1.
- The wave equation wtt = a2 wxx can be reduced to a first order
system by defining u=wt and v=wx:
ut = a2 vx
vt = ux
Solve this as a system and verify that the same solution is obtained
as we get from a canonical form of the wave equation.
- 2.
- A semi-infinite bar with unit heat conduction coefficient is initially
at zero temperature, but at the end heat is being added at a unit rate:
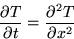
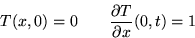
Find the temperature in the bar for arbitrary times.
- 3.
- A circular plate has an insulated circumference.
The heat conduction coefficient is unity:
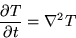
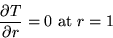
The initial temperature has an arbitrary variation.
Approximately how long will it take until the initial temperature
variations decay by a factor 10?
Your estimate for this time should be exact under certain conditions.
Which ones?
'Author: Leon van Dommelen'
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()