EML 5060 Analysis in Mechanical Engineering 11/01/19
Closed book Van Dommelen 12:30-1:20 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning.
Bare answers are absolutely not acceptable, because I will assume they
come from your calculator (or the math handbook, sometimes,) instead
of from you. You must state what result answers what part of the
question. Answer what is asked; you do not get any credit for making
up your own questions and answering those. Use the stated procedures.
Give exact, fully simplified, answers where possible.
You must use the systematic procedures described in class, not
mess around randomly until you get some answer. Echelon form is
defined as in the lecture notes, not as in the book. Eigenvalues must
be found using minors only. Eigenvectors must be found by identifying
the basis vectors of the appropriate null space. Eigenvectors of
symmetric matrices must be orthonormal. If there is a quick way to do
something, you must use it.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: Vector analysis is often the quickest and
easiest way to deal with geometry.
Question: Using vector operations only, (a) find the
area of the triangle whose corner points are A (1,1,1), B (2,2,3),
and C (3,4,5), and (b) find a scalar equation for the plane through
the three points.
Solution.
- Background: Finding eigenvalues and eigenvectors is
important for many applications such as buckling, vibrations,
principal axes, etcetera.
Question: Find the eigenvalues and eigenvectors of the following
matrix:
Use the fastest method to find the eigenvalues and state how and
why. Follow the class procedures strictly in finding the required
null spaces. No shortcuts or messing around! Make sure that every
step you take is unambigously shown. Explain all properties of
matrix 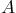 that you can get from your derived eigenvalues and
eigenvectors, without doing any other math or even looking at the
matrix itself at all (Singular? Defective? Symmetric? Rank?
Dimensions of the row, column, and null spaces?). List the
transformation matrix of the change of coordinates that makes the
matrix above diagonal, if any, and its inverse.
that you can get from your derived eigenvalues and
eigenvectors, without doing any other math or even looking at the
matrix itself at all (Singular? Defective? Symmetric? Rank?
Dimensions of the row, column, and null spaces?). List the
transformation matrix of the change of coordinates that makes the
matrix above diagonal, if any, and its inverse.
Solution.
- Background: Analyzing quadratic forms is of interest
in many applications, one of which is finding the geometry of streamlines
near a stagnation point in a flow.
Question: Consider the quadratic equation
where 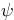 is a given constant. Using class procedures for
quadratic forms, taking the largest eigenvalue to be the first one,
first draw the solution lines in the
is a given constant. Using class procedures for
quadratic forms, taking the largest eigenvalue to be the first one,
first draw the solution lines in the 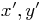 principal coordinate
system, for the cases that
principal coordinate
system, for the cases that 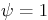 , 0, and
, 0, and 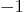 (all three in the
same plane). Then show the principal axis system, its unit vectors
(all three in the
same plane). Then show the principal axis system, its unit vectors
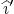 and
and 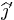 , and the solution lines in the normal
, and the solution lines in the normal 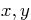 coordinate system. Fatten the solution lines or use another color.
State what
coordinate system. Fatten the solution lines or use another color.
State what 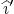 and
and 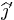 are in the
are in the 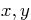 coordinate system.
Make sure the graph is qualitatively accurate and get the principal
axes intercepts and various angles as accurately as posssible.
coordinate system.
Make sure the graph is qualitatively accurate and get the principal
axes intercepts and various angles as accurately as posssible.
State how you can find the principal coordinates 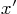 and
and 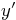 of a
point given the normal coordinates
of a
point given the normal coordinates 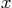 and
and  , and explain fully
how you got these relations.
, and explain fully
how you got these relations.
Solution.

![]() and
and ![]() of a
point given the normal coordinates
of a
point given the normal coordinates ![]() and
and ![]() , and explain fully
how you got these relations.
, and explain fully
how you got these relations.