EML 5060 Analysis in Mechanical Engineering 09/27/19
Closed book Van Dommelen 12:30-1:20 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare
answers are absolutely not acceptable, because I will assume they come
from your calculator (or the math handbook, sometimes,) instead of
from you. You must state what result answers what part of the
question. Answer what is asked; you do not get any credit for
making up your own questions and answering those. Ask if
clarification of what is asked is needed. Use the stated procedures.
Give exact, fully simplified, answers where possible.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: Graphical depiction of a function is often an
essential part to understand its properties.
Question: Analyze and very neatly graph
To keep it simpler, restrict yourself to 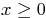 . If you find the
first derivative correctly, the numerator should be a cubic with a
root
. If you find the
first derivative correctly, the numerator should be a cubic with a
root 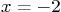 . Discuss
. Discuss  and
and  intercepts and extents, asymptotic
behavior for large positive
intercepts and extents, asymptotic
behavior for large positive  , horizontal, oblique and vertical
asymptotes, local and global maxima and minima, concavity,
inflection points, kinks, cusps, vertical slopes and other
singularities.
, horizontal, oblique and vertical
asymptotes, local and global maxima and minima, concavity,
inflection points, kinks, cusps, vertical slopes and other
singularities.
Draw the function very neatly and precisely, on suitably labelled
axes, clearly showing all features.
Solution.
- Background: Sometimes you may need to evaluate a function
for which no library function is readily available. A Taylor series
may then be convenient.
Question: The sine integral
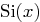 is the function which is zero at
is the function which is zero at 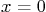 and whose derivative is
the
and whose derivative is
the sinc
function 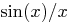 . In other words,
. In other words,
Write the Maclaurin series for 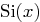 by writing the
Maclaurin series for the integrand in the integral above and then
integrating that. Write both the first four nonzero terms in the
series explicitly, as well as all infinitely many terms, the latter
by using a summation symbol.
by writing the
Maclaurin series for the integrand in the integral above and then
integrating that. Write both the first four nonzero terms in the
series explicitly, as well as all infinitely many terms, the latter
by using a summation symbol.
Solution.
- Background: Centroids of plates are important for dynamics,
hydrostatics, etcetera.
Question: Find the integral 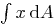 for the
region
for the
region
using the normal polar coordinates. Write the complete integrals,
including integration limits, if you do 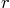 first and if you do
first and if you do
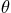 first. Then work out one of these two integrals.
first. Then work out one of these two integrals.
Solution.
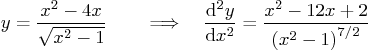
![]() is the function which is zero at
is the function which is zero at ![]() and whose derivative is
the
and whose derivative is
the ![]() . In other words,
. In other words,
![]() for the
region
for the
region