EML 5060 Analysis in Mechanical Engineering I 12/10/19
Closed book Van Dommelen 5:30-7:30 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare
answers are absolutely not acceptable, because I will assume they come
from your calculator (or the math handbook, sometimes,) instead of
from you. You must state what result answers what part of the
question. Answer exactly what is asked; you do not get any credit for
making up your own questions and answering those. Use the stated
procedures. Give exact, fully simplified, answers.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: Dynamical systems, even if nonlinear, are
typically described by differential equations. First order scalar
equations can often be solved exactly (if they have some simplifying
feature).
Question: As a simple example, solve the nonlinear ordinary
differential equation
using the class procedures for this type of equation. Write
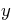 as a function of
as a function of 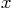 . Neatly and accurately sketch the curve
for
. Neatly and accurately sketch the curve
for 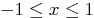 if
if 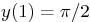 , labeling the axes appropriately.
(If there are any multiple valued functions in your solution, use
the principal branch.)
, labeling the axes appropriately.
(If there are any multiple valued functions in your solution, use
the principal branch.)
Solution.
- Background: Vibrating systems are typically described by
differential equations. For small amplitudes, these can often
be solved exactly.
Question: Using variation of parameters and the other class
procedures, including showing clean up procedures, solve the forced
vibrating system
Solution.
- Background: Nonlinear dynamical systems often cannot be
solved analytically. However, valuable qualitative understanding
can often be obtained using critical (stationary) point analysis.
Question: Consider the following equation for a damped vibrating system
with a spring that softens when extended:
Convert this equation in a first order system, then show that that system
has only one stationary point, and that at the stationary point,
the linearized problem takes the form
Solve this system using the class procedures for systems. Then very
accurately and neatly draw a typical solution line near the
stationary point. Show the governing vectors. Make sure angles and
slopes are right. Classify the stationary point. Could the
stationary point analysis be qualitative wrong? Explain all.
Solution.