EML 5060 Analysis in Mechanical Engineering 11/17/17
Closed book Van Dommelen 12:30-1:20 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare
answers are absolutely not acceptable, because I will assume they come
from your calculator (or the math handbook, sometimes,) instead of
from you. You must state what result answers what part of the
question. Answer what is asked; you do not get any credit for making
up your own questions and answering those. Use the stated procedures.
Give exact, fully simplified, answers where possible.
You must use the systematic procedures described in class, not
mess around randomly until you get some answer. Echelon form is
defined as in the lecture notes, not as in the book. Eigenvalues must
be found using minors only. Eigenvectors must be found by identifying
the basis vectors of the appropriate null space. Eigenvectors of
symmetric matrices must be orthonormal. If there is a quick way to do
something, you must use it.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: In finite volume fluid computations, the flow
field may be divided into simple volumes, and you then need to find
expressions for the surfaces of these volumes and the volumes.
Question: Assume that point A has Cartesian coordinates
(1,2,3), B (4,4,4), C (3,3,5), and D (2,3,5). Find the area of the
parallelogram that has AB and AC as sides. Also find a vector of
unit length normal to that parallelogram. Also find the volume of
the parallelepiped with sides AB, AC, and AD.
Solution.
- Background: The eigenvalues of the
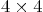 Dirac matrix
Dirac matrix
describe the possible energies of an electron moving in free space,
where 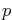 is the scaled linear momentum of the electron. (Here
is the scaled linear momentum of the electron. (Here 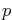 is real, not complex.)
is real, not complex.)
Question: Find the four eigenvalues of the matrix above. Do
not use any Gaussian elimination steps. Note: the quartic is easy
to factor, and in any case it can be written as a quadratic in terms
of 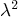 . Without solving for the eigenvectors, what can you
say about the diagonalizability of the Dirac matrix and why?
. Without solving for the eigenvectors, what can you
say about the diagonalizability of the Dirac matrix and why?
Solution.
- Background: Many problems in physics require analysis of
quadratic forms. Linear algebra is the general way to do so. Here
we will restrict ourselves to a two-dimensional form, though in real
life, the number of dimensions might be enormous.
Question: Analyze the quadratic form
using class procedures. Based on that, very neatly draw the
solution curve(s) in the 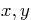 -plane. In particular, show the
principal axes, the unit vectors along the principal axes, principal
axes intercepts, if any, asymptotes, if any, and all angles involved
as accurately as reasonably possible, listing their exact and
approximate values.
-plane. In particular, show the
principal axes, the unit vectors along the principal axes, principal
axes intercepts, if any, asymptotes, if any, and all angles involved
as accurately as reasonably possible, listing their exact and
approximate values.
Solution.
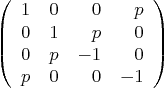
![]() . Without solving for the eigenvectors, what can you
say about the diagonalizability of the Dirac matrix and why?
. Without solving for the eigenvectors, what can you
say about the diagonalizability of the Dirac matrix and why?