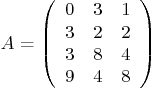EML 5060 Analysis in Mechanical Engineering 11/04/16
Closed book Van Dommelen 12:30-1:20 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare
answers are absolutely not acceptable, because I will assume they come
from your calculator (or the math handbook, sometimes,) instead of
from you. You must state what result answers what part of the
question. Answer exactly what is asked; you do not get any credit for
making up your own questions and answering those. Use the stated
procedures. Give exact, fully simplified, answers.
You must use the systematic procedures described in class, not
mess around randomly until you get some answer. Echelon form is
defined as in the lecture notes, not as in the book. Eigenvalues must
be found using minors only. Eigenvectors must be found by identifying
the basis vectors of the appropriate null space. Eigenvectors to
symmetric matrices must be orthonormal. If there is a quick way to do
something, you must do it.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background:
Vector analysis of geometry is of importance in many areas of
mechanical engineering, including manufacturing, mechanisms and
design.
Question: Find the equation of the line through the point P,
(1,2,3), that hits the plane 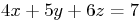 orthogonally. Give the
equation of the line both in vector form and in terms of its
orthogonally. Give the
equation of the line both in vector form and in terms of its 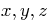 coordinates only.
coordinates only.
Use vector analysis only, including the appropriate vector products
if needed. (Do not use trig, say.)
Solution.
- Background: If your truss will only need to support
specific types of forces, you may leave out some bars. In that case
you can study the force combinations that the struss can still
support by finding a simplified basis for the column space of
the associated equilibrium matrix.
Question: Find a simplified basis for the column space
of
Any reduction to echelon form involved must be strictly according to
class procedures and you must avoid fractions in it. List
separately the simplified basis of the column space and the
simplified column space.
Solution.
- Background: Analyzing quadratic forms appears, for example,
in the examination of the elastic behavior of structures.
Question: As a small example, use class procedures to analyze the
quadratic form
In particular, describe the shape of the surface, whether it is a
surface of revolution, the unit axial vectors of the principal
coordinate system, and the intercepts / axis lengths / asymptotic
surfaces, whatever applies.
Solution.
![]() orthogonally. Give the
equation of the line both in vector form and in terms of its
orthogonally. Give the
equation of the line both in vector form and in terms of its ![]() coordinates only.
coordinates only.