EML 5060 Analysis in Mechanical Engineering 11/01/13
Closed book Van Dommelen 11:50-12:40 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare answers
are absolutely not acceptable, because I will assume they come from
your calculator (or the math handbook, sometimes,) instead of from
you. You must state what result answers what part of the question if
there is any ambiguity. Answer exactly what is asked; you do not get
any credit for making up your own questions and answering those. Use
the stated procedures. Give exact, fully simplified, answers where
possible.
You must use the systematic procedures described in class, not
mess around randomly until you get some answer. Eigenvalues must be
found using minors only. Eigenvectors must be found by identifying
the basis vectors of the appropriate null space if there are multiple
eigenvalues. Eigenvectors to symmetric matrices must be orthonormal.
If there is a quick way to do something, you must do it.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: Typically, if you use too few bars in a
truss, it will not be able to support the required applied forces.
If you use too many bars, there will typically be
residual
tension forces in the bars even if no
forces are applied. These can be big and lead to unexpected
failure.
Question: A truss was designed to support the three externally
applied force components 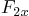 ,
, 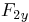 , and
, and 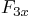 . The
truss consists of four bars, under tension forces
. The
truss consists of four bars, under tension forces 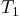 ,
, 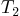 ,
,
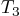 , and
, and 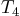 respectively. These tension forces relate to the
applied forces as
respectively. These tension forces relate to the
applied forces as
What makes you suspect immediately that the designer may not come
from a very good Engineering school? Write the system in a suitable
matrix form. Solve it using class procedures and also find the null
space. Based on the results, address what of the two potential problems
mentioned above, if any, might affect this truss. What do you learn
in more detail from the structure of the null space?
Solution.
- Background: For purposes such as analyzing natural
frequencies, or in quantum mechanics, sometimes an analytical
expression of a determinant is needed.
Question: Find, without any row (or column) operations
At every stage, choose the approach that requires the smallest
possible number of terms. If you do it correctly, it will be quick.
Solution.
- Background: If an appropriate streamfunction exists for a
flow, then the streamlines in the vicinity of stagnation points can
be found as lines on which a quadratic form is constant.
Question: Using the class procedures for quadratic forms, find
and very accurately and neatly draw the lines on which 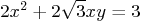 . List all relevant angles in the picture to fully define it.
Describe the points that come closest to the origin, and their
distance from the origin.
. List all relevant angles in the picture to fully define it.
Describe the points that come closest to the origin, and their
distance from the origin.
Solution.
![]() ,
, ![]() , and
, and ![]() . The
truss consists of four bars, under tension forces
. The
truss consists of four bars, under tension forces ![]() ,
, ![]() ,
,
![]() , and
, and ![]() respectively. These tension forces relate to the
applied forces as
respectively. These tension forces relate to the
applied forces as

![]() . List all relevant angles in the picture to fully define it.
Describe the points that come closest to the origin, and their
distance from the origin.
. List all relevant angles in the picture to fully define it.
Describe the points that come closest to the origin, and their
distance from the origin.