EML 5060 Analysis in Mechanical Engineering 12/10/13
Closed book Van Dommelen 10-12 noon
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare
answers are absolutely not acceptable, because I will assume they come
from your calculator (or the math handbook, sometimes,) instead of
from you. You must state what result answers what part of the
question if there is any ambiguity. Answer exactly what is asked; you
do not get any credit for making up your own questions and answering
those. Use the stated procedures. Give exact, fully simplified,
answers where possible.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: Consider a sphere moving in a viscous fluid.
The viscosity of the fluid is increasing linearly in time as its
gets hotter. A force is applied that grows proportional to the
viscosity. The velocity
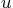 of such a sphere is described by
of such a sphere is described by
where 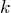 and
and 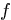 are positive constants.
are positive constants.
Question: Solve the above system using the class
procedure for linear 1st order equations. Graph some
representative solution curves versus time. What can you say about the
long-time behavior of the velocity?
Solution.
- Background: The Laplace transform is one way of solving
complicated dynamical systems. One strength is its capability of
analyzing the stability properties. The simplest dynamical system
is of course the one-dimensional spring mass system
where 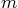 is the mass,
is the mass, 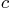 the damping constant,
the damping constant, 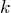 the spring
constant, and
the spring
constant, and  the applied force.
the applied force.
Question: Solve the above system using the Laplace transform
if 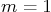 ,
, 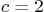 ,
,  , and
, and  is some given function of time.
Take
is some given function of time.
Take 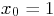 and
and 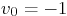 .
.
A table of Laplace transforms is attached. Everything not in this
table must be fully derived showing all reasoning. The convolution
theorem may only be used where it is absolutely unavoidable. Do not
use any complex numbers in your analysis (besides  .)
.)
Solution.
- Background: In steady fluid flows, the fluid motion
satisfies, of course,
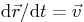 . Near a
. Near a
stagnation point
, the right hand side can be
linearized to show the local motion.
Question: Solve using class procedures for 1st order systems:
which would be a possible example in two dimensions.
Draw the solution curves in the  -plane very neatly and
quantitatively reasonably accurately. You should have 2 examples of
each different type of curve, or 1 if there is just one curve of
that type. Be sure to put an arrow in the direction of motion on
each curve.
-plane very neatly and
quantitatively reasonably accurately. You should have 2 examples of
each different type of curve, or 1 if there is just one curve of
that type. Be sure to put an arrow in the direction of motion on
each curve.
Make sure that you check your algebra carefully. You do not get
credit for making the wrong graph.
Solution.
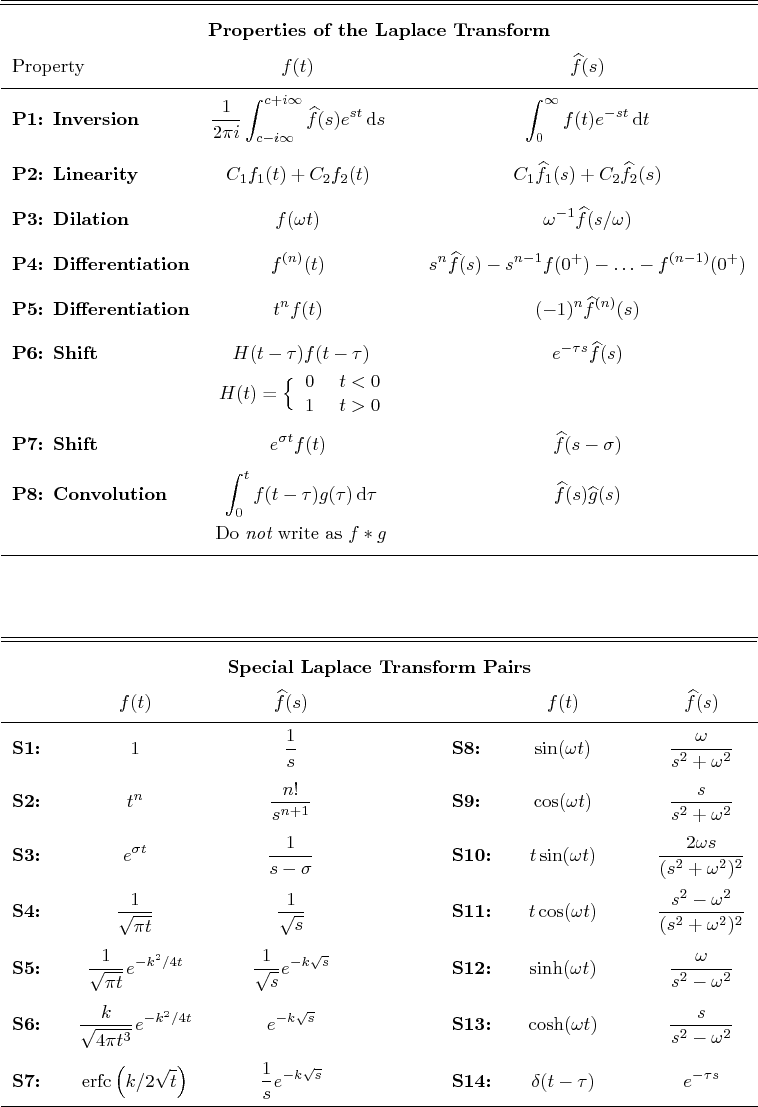
Table 1:
Properties of the Laplace Transform.
(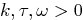 ,
, 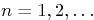 )
)
|
|
![]() ,
, ![]() ,
, ![]() , and
, and ![]() is some given function of time.
Take
is some given function of time.
Take ![]() and
and ![]() .
.
![]() .)
.)
![]() -plane very neatly and
quantitatively reasonably accurately. You should have 2 examples of
each different type of curve, or 1 if there is just one curve of
that type. Be sure to put an arrow in the direction of motion on
each curve.
-plane very neatly and
quantitatively reasonably accurately. You should have 2 examples of
each different type of curve, or 1 if there is just one curve of
that type. Be sure to put an arrow in the direction of motion on
each curve.