EML 5060 Analysis in Mechanical Engineering 9/23/09
Closed book Van Dommelen 11:50-12:40 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare answers
are absolutely not acceptable, because I will assume they come from
your calculator (or the math handbook, sometimes,) instead of from
you. You must state what result answers what part of the question if
there is any ambiguity. Answer exactly what is asked; you do not get
any credit for making up your own questions and answering those. Use
the stated procedures. Give exact, cleaned-up, answers where
possible.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: Graphical depiction of a function is often an
essential part to understand its properties.
Question: Analyze and very neatly graph
Discuss 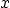 and
and  intercepts and extents, horizontal, oblique and
vertical asymptotes, symmetries, local and global maxima and minima,
kinks, cusps, horizontal and vertical slopes. Given that there is
only one inflection point in the curve, where is it?
intercepts and extents, horizontal, oblique and
vertical asymptotes, symmetries, local and global maxima and minima,
kinks, cusps, horizontal and vertical slopes. Given that there is
only one inflection point in the curve, where is it?
Solution.
- Background: Some functions cannot be evaluated in terms of
elementary functions and numerical techniques must be used.
Question: Derive the value of
Terminate evaluating terms as soon as you have ensured an error of
no more than 0.0005. Give the best possible estimate for what is the
precise error in you answer at that time.
Solution.
- Background: Moments of inertia are key to fields like
dynamics and hydrostatics.
Question: Evaluate
over the first quadrant area below the parabola  and inside
the circle
and inside
the circle 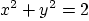 that intersects the parabola at (1,1). Make
a very neat graph of the region of integration.
that intersects the parabola at (1,1). Make
a very neat graph of the region of integration.
Solution.