EML 5060 Analysis in Mechanical Engineering 12/12/08
Closed book Van Dommelen 7:30-9:30 am
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare answers
are absolutely not acceptable, because I will assume they come from
your calculator (or the math handbook, sometimes,) instead of from
you. You must state what result answers what part of the question if
there is any ambiguity. Answer exactly what is asked; you do not get
any credit for making up your own questions and answering those. Use
the stated procedures. Give exact, cleaned-up, answers where
possible.
One book of mathematical tables, such as Schaum’s Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet. The Laplace tables of the book are
attached.
- Background: In the approximate Pohlhausen method for
boundary layers, the following ODE arises
where 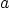 and
and 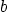 are given constants
are given constants
Question: Solve the above ODE using the class procedures for
this type of ODE. Assume
Solution.
- Background: Laplace transforms are a good way to solve
dynamical systems, especially when their large-time behavior or
stability is of interest.
Question: Solve
using the class Laplace transform procedures. Make sure there is no
funny mathematics in your final answer. It must be phrased in
simple terms that the instructor can understand.
Solution.
- Background: First order systems of ODE have the advantage
that they can be used regardless of the size of your dynamic system
and its nonlinearity.
Question: Consider a simple case; that of a mass spring-system
with nonlinear damping:
- Explain how this second order equation can be reduced to the
first order system
- Explain why information about this nonlinear system can be
obtained from solving the following, single, linear system:
and identify 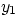 and
and 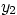 .
.
- Solve the linear system using class procedures for constant
coefficient first order systems.
- Classify the type of point and its stability.
- Verify that you got it right based on the determinant/trace
plot.
- Very neatly and quantitatively correct, draw three
representative solution curves. Show the direction of time
evolution using arrows.
- Is the linear system theoretically guaranteed to correctly
predict the behavior of the nonlinear one? Sketch in a
separate phase plane what you expect for the nonlinear system.
Solution.