|
|
|
Solutions should be fully derived showing all intermediate results, using class procedures. Show all reasoning. Bare answers are absolutely not acceptable, because I will assume they come from your calculator (or the math handbook, sometimes,) instead of from you. You must state what result answers what part of the question if there is any ambiguity. Answer exactly what is asked; you do not get any credit for making up your own questions and answering those.
You must use the systematic procedures described in class, not mess around randomly until you get some answer. Geometry must be done using vector operations. Use standard matrix methods to determine linear independence and simplified bases of vector spaces. You need to reduce matrices to echelon form where elimination is called for, using the basic row operations and following the class procedures. Do not take shortcuts. Do not reduce further if there is no need. Eigenvalues must be found using minors only. Eigenvectors must be found by identifying the basis vectors of the appropriate null space if there are multiple eigenvalues, using the appropriate procedures. Eigenvectors to symmetric matrices must be orthonormal. Higher matrix powers and polynomials must be found through transformation, not crunching. Inverses must be found the quick way, where possible.
One book of mathematical tables, such as Schaum's Mathematical Handbook, may be used, as well as a calculator, and a handwritten letter-size formula sheet.
Question: Assuming that point A has coordinates (1,2,3), B (1,1,1), and C (2,4,6), find the area of the parallelogram that has BA and BC as sides. Also find a vector of unit length normal to the parallelogram.
Question: Find a complete set of eigenvalues and eigenvectors
to the following matrix, using the required procedures:
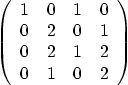
Question: Consider the quadratic form