EML 5060 Analysis in Mechanical Engineering 12/11/07
Closed book Van Dommelen 10:00-12:00 EDT
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare answers
are absolutely not acceptable, because I will assume they come from
your calculator (or the math handbook, sometimes,) instead of from
you. You must state what result answers what part of the question if
there is any ambiguity. Answer what is asked; you do not get any
credit for making up your own questions and answering those. Use the
stated procedures.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: The following ODE arises in the analysis of
hedging of variable annuities:
Question:
- Derive the general solution of the homogeneous equation.
- Derive the general solution of the inhomogeneous equation.
- Very neatly draw an exhaustive set of solution curves, and
then some more, of the inhomogeneous equation for the case that
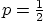 . (Note that
. (Note that 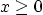 .)
.)
- Find the solution when
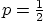 and
and 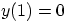 .
.
- Comment on the initial value problem in which
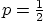 and
and
 .
.
Solution.
- Background: Vibrations of simple systems are governed by
the ODE:
where 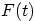 is some given time-varying force acting on the system.
is some given time-varying force acting on the system.
Question: Derive the solution of this equation if 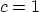 ,
,
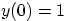 , and
, and 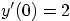 , by means of Laplace transformation. Work
out completely; there may not be a
, by means of Laplace transformation. Work
out completely; there may not be a  or
or  in the answer. You
must use the completion of the square method in this problem.
in the answer. You
must use the completion of the square method in this problem.
Solution.
- Background: The following nonlinear system describes
a biased Van der Pol oscillator:
Question:
- Explain why we can learn information about the solutions
of this system by studying the following system:
In particular, identify 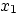 and
and 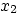 .
.
- Write the general solution for
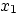 and
and 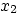 .
.
- Very neatly and quantitatively correct, draw an exhaustive set
of solution curves in the
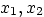 -plane. Make sure all
qualitative features are clearly visible.
-plane. Make sure all
qualitative features are clearly visible.
- Classify the point precisely.
- Explain whether or not these solution curves are relevant
to the solution curves of the original problem. If they
are, in what sense they are relevant. If the relevance is not
quite certain, indicate so.
- What can be said about the long-time behavior of typical
solutions of the original system based on the obtained results?
Solution.
![]() ,
,
![]() , and
, and ![]() , by means of Laplace transformation. Work
out completely; there may not be a
, by means of Laplace transformation. Work
out completely; there may not be a ![]() or
or ![]() in the answer. You
must use the completion of the square method in this problem.
in the answer. You
must use the completion of the square method in this problem.