|
|
|
Solutions should be fully derived showing all intermediate results, using class procedures. Show all reasoning. Bare answers are absolutely not acceptable, because I will assume they come from your calculator (or the math handbook, sometimes,) instead of from you. You must state what result answers what part of the question if there is any ambiguity. Answer exactly what is asked; you do not get any credit for making up your own questions and answering those.
You must use the systematic procedures described in class, not mess around randomly until you get some answer. Do not take shortcuts. Some reminders: You need to reduce matrices completely to echelon form where appropriate to the question, (but not to row canonical if it would be inefficient for large matrices), using the procedure given in class, find the basis of the null spaces and orthonormalize eigenvectors using modified Gram-Schmidt where appropriate, etcetera. Do not throw away zero rows in Gaussian elimination. Coordinate transformations must be found using transformation matrices only. Coordinate transformations for symmetric matrices must be orthonormal. Inverses of unitary matrices must be found by transposing. Principal axes and principal values must be found as eigenvalue problems using class procedures. Polynomials of matrices above degree 2 must be found using diagonalization. Quadratic forms must be reduced using class procedures.
One book of mathematical tables, such as Schaum's Mathematical Handbook, may be used, as well as a calculator, and a handwritten letter-size formula sheet.
Question: Find a basis of the null space of the matrix
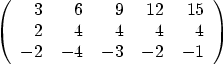
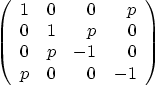
Question: Find the eigenvalues of the matrix above. Do not use any Gaussian elimination. Without solving for the eigenvectors, what can you say about the diagonalizability of the Dirac matrix and why?
Question: Find the approriate new unknowns ![]() and
and ![]() in
terms of which
in
terms of which ![]() above can be written without an
above can be written without an ![]() term.
Graphically show the relationship between the coordinates
term.
Graphically show the relationship between the coordinates ![]() and
and
![]() .
.