EML 5060 Analysis in Mechanical Engineering 9/27/06
Closed book Van Dommelen 11:50-12:40 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Bare answers are absolutely not
acceptable, because I will assume they come from your calculator (or
the math handbook, sometimes,) instead of from you. You must state
what result answers what part of the question if there is any
ambiguity. Answer exactly what is asked; you do not get any credit
for making up your own questions and answering those.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: The curved surface of a barrel will be more
expensive to make than the top and bottom. This question intends to
find the most economical dimensions if the cost per square feet of
the curved surface is twice that of the flat bottom and top
surfaces.
Question: If for a cylindrical container, the cost of the
cylindrical surface is $4/ft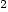 and that of the top and bottom
circles is $2/ft
and that of the top and bottom
circles is $2/ft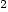 , then what is the lowest possible cost
of a barrel that is to hold 10 ft
, then what is the lowest possible cost
of a barrel that is to hold 10 ft ?
?
Solution.
- Background: In the Lagrangian description of an established
unsteady separation point, the position of the particles at the
separation position can be written as
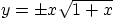 .
.
Question: Analyze and graph very neatly the curve
Discuss presence or absence of  -and
-and 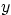 - intercepts, local maxima
and minima, global maxima and minima, vertical, oblique, and
horizontal asymptotes, vertical slopes, cusps, and kinks, and give
- intercepts, local maxima
and minima, global maxima and minima, vertical, oblique, and
horizontal asymptotes, vertical slopes, cusps, and kinks, and give
 and
and 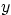 extents. Features that are unclear or ambiguous in
the graph count as failed. Note: you do not have to discuss
inflection points.
extents. Features that are unclear or ambiguous in
the graph count as failed. Note: you do not have to discuss
inflection points.
Solution.
- Background: Unlike you might think from the book, finding
centroids and moments of inertia of plates is not always just a
matter of integrating powers of
 and
and 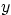 . If the thickness or
material density vary, any integral may show up.
. If the thickness or
material density vary, any integral may show up.
Question: Integrate
over the surface bounded by  ,
,  , and
, and
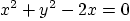 .
Hint: Use polar coordinates.
.
Hint: Use polar coordinates.
Solution.
![]() and that of the top and bottom
circles is $2/ft
and that of the top and bottom
circles is $2/ft![]() , then what is the lowest possible cost
of a barrel that is to hold 10 ft
, then what is the lowest possible cost
of a barrel that is to hold 10 ft![]() ?
?