EML 5060 Analysis in Mechanical Engineering 10/17/03
Closed book Van Dommelen 9:15-10:05 pm

One book of mathematical tables, such as Schaum's Mathematical Handbook, may be used, as well as a calculator and a single handwritten sheet of formulae.

Show all reasoning and intermediate results leading to your answer, or credit will be lost. I must be able to see clearly how you derived everything, and you must state what the result you derived is in terms of what is asked. Answer exactly what is asked; you do not get credit for making up your own questions and answering those. You must use the systematic procedures followed in class, not mess around randomly until you get some answer. Do not take shortcuts. For example, you need to reduce matrices completely to echelon form where appropriate to the question, find the basis of null spaces, orthonormalize eigenvectors where appropriate, etc. etc.

1.

The table below shows gives the length of an automotive spring for three different forces F applied to the spring:

1 5

2 7

3 10

The spring behavior is to be represented by an expression of the form 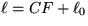where the inverse spring stiffness C and the nominal length of the spring 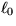are to be found. Each of the three rows in the table above gives an equation for the two unknowns C and 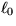. Write this system of equations in the form 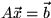, where 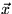is the vector of unknowns 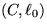. This system does not have a solution. We can however premultiply by the transpose matrix to get the system . Find the matrix A^T A and right hand side 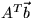of this system of equations and solve it using class procedures. The solution will be the least squares solution.

Solution.

2.

If we write continuity for the piping system shown below, we get the following equations for the unknown mass flows in the pipes , , , :

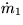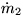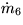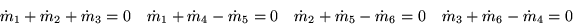
Find a basis for the null space of the above system, with the unknowns in the given order, using the class procedures. The basis vectors represent the basic flow patterns that the general solution consists of. Sketch those basic flow patterns.

Solution.

3.

The equations of motion for the three mass system shown below are:

Take m=k=1 and find the mode shapes in the way we did class for the double pendulum. In other words, assume that (x₁,x₂,x₃)^T is where is a constant vector that gives the mode shapes, and find the possible vectors .

Solution.