EML 5060 Analysis in Mechanical Engineering 12/11/03
Closed book Van Dommelen 3:00-5:00 pm

Solutions should be fully derived using class procedures: be sure to show your complete derivation, not just the answer. ``My calculator / mathematical handbook says that this is the solution'' is not acceptable. You must state what result of yours answers what part of the question if there is any ambiguity. Answer exactly what is asked; you do not get any credit for making up your own questions and answering those.

One book of mathematical tables, such as Schaum's Mathematical Handbook, may be used, as well as a calculator, and a handwritten letter-size formula sheet.

1.

Small-scale perturbations in a supersonic flow satisfy the following PDE for the perturbation pressure p(x,y,z):

(u² - a²) p_xx + (v² - a²) p_yy + (w² - a²) p_zz + 2 u v p_xy + 2 v w p_yz + 2 w u p_zx = 0

where a is the speed of sound, which is to be assumed constant, and (u,v,w) is the supersonic flow velocity; take it as (u,v,w)=(2a,a,a). Derive the simplified canonical equation by rotating the coordinate system using class PDE transformation procedures. Give the simplified equation and the new coordinate system. Explain why the results you obtained could have been expected physically without doing the math.

Solution.

2.

Find the unsteady temperature distribution u(x,t) in a bar extending from x=0 to 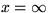, if the initial temperature at time t=0 is zero, and the end at x=0 is held at 5 degrees centigrade for 0<t<1 and at zero degrees for 1<t. The heat conduction coefficient is 9 m²/s. Be sure to simplify your answer and write it in terms of what is given only.

Solution.

3.

Find the unsteady temperature distribution u(x,t) in a bar of length 3 m if the end at x=0 m is held at 15 degrees Centigrade, while the other end at x=3 m is insulated (i.e. it has a homogeneous Neumann boundary condition.) Assume the initial temperature to be of the form u(x,0)=f(x) where f(x)=20 C in the range 0 m<x<1 m and f(x)=15 C for 1 m<x<3 m. The heat conduction coefficient is 9 m²/s

Solution.

4.

Answer the preassigned PDE problem. Your solution may be brought into the exam.

Solution.