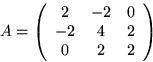Up: Return
EML 5060 Analysis in Mechanical Engineering 9/20/02
Closed book Van Dommelen 11:50-12:40 pm
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. I must be able to see clearly how you
derived everything, and you must state what the result you
derived is in terms of what is asked. Answer exactly what is
asked; you do not get credit for making up your own questions
and answering those. You must use the systematic procedures
followed in class, not mess around randomly until you get some
answer. For example, you need to reduce matrices completely to
echelon form where appropriate to the question, orthonormalize
eigenvectors where appropriate, etcetera. One book of mathematical
tables, such as Schaum's Mathematical Handbook, may be used, as well
as a calculator.
- 1.
- To solve the large systems of equations generated by numerical schemes,
the general-purpose method is reduction to echelon form. Reduce the
matrix

to echelon form.
Solution.
- 2.
- The degrees of freedom of a simple vibrating system are a linear
displacement x and an angular one
 . To solve the
vibration problem, we first make the following transformation to new
coordinates q1 and q2:
. To solve the
vibration problem, we first make the following transformation to new
coordinates q1 and q2:
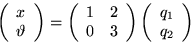
Identify the basis vectors of the (q1,q2) coordinate system
in terms of the  coordinate system. Also give the
transformation matrix from the (q1,q2) system to
the
coordinate system. Also give the
transformation matrix from the (q1,q2) system to
the  system. Next, solving the (symmetric matrix) eigenvalue
problem in the (q1,q2) coordinate systems, the solution
can be written
system. Next, solving the (symmetric matrix) eigenvalue
problem in the (q1,q2) coordinate systems, the solution
can be written
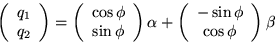
where 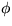 is some constant you can leave as
is some constant you can leave as 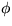 .
Find the transformation matrix from
.
Find the transformation matrix from 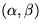 coordinates to
coordinates to  coordinates.
coordinates.
Solution.
- 3.
- The inertia matrix of a thin long solid body,
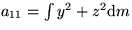 ,
,
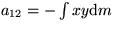 , etcetera, is found nuerically as
, etcetera, is found nuerically as
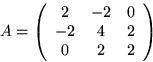
Find the basis vectors 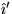 ,
, 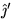 ,
, 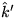 of a
rotated Cartesian coordinate system in which the off-diagonal moments
of inertia are zero. Also identify the remaining nonzero moments of inertia
(called the principal moments of inertia.) Do you think my numerical
integration may have been inaccurate?
Solution.
of a
rotated Cartesian coordinate system in which the off-diagonal moments
of inertia are zero. Also identify the remaining nonzero moments of inertia
(called the principal moments of inertia.) Do you think my numerical
integration may have been inaccurate?
Solution.
Up: Return

![]()
![]()
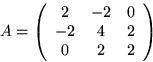

![]()
![]()