EML 5060 Analysis in Mechanical Engineering 12/11/02
Closed book Van Dommelen 12:30-2:30 pm

Show all reasoning and intermediate results leading to your answer, or credit will be lost. I must be able to see clearly how you derived everything, and you must state what the result you derived is in terms of what is asked. Answer exactly what is asked; you do not get credit for making up your own questions and answering those. You must use the systematic procedures followed in class, not mess around randomly until you get some answer. Clean up as much as possible. One book of mathematical tables, such as Schaum's Mathematical Handbook, may be used, as well as a calculator and a handwritten letter-size formula sheet.

1.

Find the temperature in a bar of length 1 if the bar is at zero temperature at time t=0, but for t>0 the temperature of the ends is equal to t. Take the heat conduction coefficient to be 1. From the results, give a simple approximation for the temperature at large times that has a vanishingly small error.

Solution.

2.

Find the decay of an asymptotic suction boundary layer when the suction is terminated and the wall is allowed to move with the flow. This problem is governed by the following equations for the unknown u(x,t):

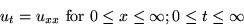
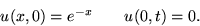
Note that, unlike usually, the initial condition is here nonzero.

Solution.

3.

The initial displacement u(x,0) of a string is 1, (really only by approximation), except at the ends at x=0 and x=1, where the displacement is zero at all times; u(0,t)=u(1,t)=0. The initial velocity is zero. The wave propagation speed a=1. Find the displacement u at x=0.5 and t=3. What sort of values can u(x,t) have in general?

Solution.

4.

Answer the preassigned PDE problem.

Solution.