Up: Return
EML 5060 Analysis in Mechanical Engineering 9/19/01
Closed book Van Dommelen 10:35-11:25am
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator. Follow
the standard procedures; don't mess around at random.
- 1.
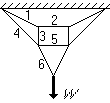
- A weight W is hung from the ceiling by a net of ropes as
shown. The equilibrium equations governing the tension forces in
the ropes are:
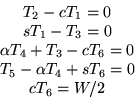
where 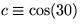 ,
,  and
and
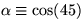 Using the systematic procedures used in this
class, solve this system and find the general solution for the
tension forces in the ropes in as simple and clear a form as
possible. Keep the given order of the equations; do not use partial
pivoting. Using the result, identify a rope that you could leave
out and still be able to suspend any weight. Check that the tension
forces in all the ropes are nonnegative: ropes cannot support
compressive forces.
Using the systematic procedures used in this
class, solve this system and find the general solution for the
tension forces in the ropes in as simple and clear a form as
possible. Keep the given order of the equations; do not use partial
pivoting. Using the result, identify a rope that you could leave
out and still be able to suspend any weight. Check that the tension
forces in all the ropes are nonnegative: ropes cannot support
compressive forces.
Solution.
- 2.
- Air above the sea is moving with a wind velocity
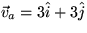 . The sea water is moving with a velocity
. The sea water is moving with a velocity 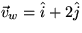 . To study the motion of small particles
that fall into the sea, special coordinates can be useful: Instead
of describing the position of these particles using the conventional
Cartesian coordinates x and y, it is easier to describe their
position vector using the air and water velocities as basis vectors:
. To study the motion of small particles
that fall into the sea, special coordinates can be useful: Instead
of describing the position of these particles using the conventional
Cartesian coordinates x and y, it is easier to describe their
position vector using the air and water velocities as basis vectors:
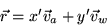
since changes in x' and y' are simply the amounts of time spend
in air and water respectively. Find the formulas that give the
coordinates x and y if we know x' and y'. Also find the
formulas that give the coordinates x' and y' if we know x and
y.

Solution.
- 3.
- The two coupled pendulae shown satisfy the following equations
of motion:
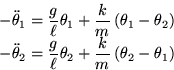
Assume 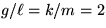 Show that solutions of the form:
Show that solutions of the form:

lead to an standard eigenvalue problem. Identify the matrix,
eigenvector, and eigenvalue. Describe the motion(s) corresponding to
the solution(s) of this eigenvalue problem.
Solution.
Up: Return
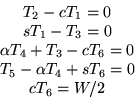

![]()

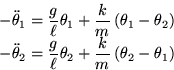
![]()

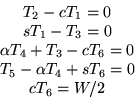

![]()

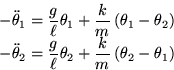
![]()
