Up: Return
EML 5060 Analysis in Mechanical Engineering 9/19/01
Closed book Van Dommelen 10:35-11:25am
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator.
- 1.
- When numerically solving partial differential equations on a
computer, normally a ``mesh'' of points must be defined. Algebraic
mesh generation requires that certain functions are chosen to define
the mesh. In one of my programs, I am using, in part, the following
function:
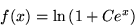
where C is a constant.
The reason I am using this function is that it has a horizontal
asymptote for large negative x and has a 45 degree asymptote for
large positive x. Do the following:
- (a)
- Verify the horizontal asymptote at large negative
x by finding
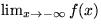 . (The value
of this limit is the height of the asymptote.)
. (The value
of this limit is the height of the asymptote.)
- (b)
- Find the y-intercept of the 45 degree asymptote.
This intercept is given as the limit for
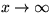 of
the following function:
of
the following function:
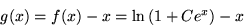
(Hint: you might want to find the limit of the
function eg first.)
(The fact that the intercept exists verifies that f
does indeed have a 45 degree asymptote.)
Solution.
- 2.
- The rim angle
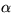 of a solar energy collector made up
out of plane mirrors satisfies the equation:
of a solar energy collector made up
out of plane mirrors satisfies the equation:
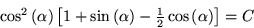
where C is a constant that depends on the desired concentration
factor, mirror density, height, etcetera. Assuming that 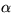 is small, (i.e. that C is close to a half), write an approximate cubic
equation for the rim angle
is small, (i.e. that C is close to a half), write an approximate cubic
equation for the rim angle 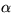 . (You do not have to solve
the cubic equation unless you want to.)
. (You do not have to solve
the cubic equation unless you want to.)
Solution.
- 3.
- Find the moment of inertia
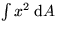 for
the flattened axis
for
the flattened axis 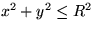 and
and  .
.
Solution.
Up: Return
![]()
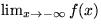 . (The value
of this limit is the height of the asymptote.)
. (The value
of this limit is the height of the asymptote.)
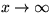 of
the following function:
of
the following function:
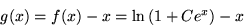
![]()