EML 5060 Analysis in Mechanical Engineering 12/15/00
Closed book Van Dommelen 10:00-12:00 noon

Show all reasoning and intermediate results leading to your answer, or credit will be lost. One book of mathematical tables, such as Schaum's Mathematical Handbook, may be used, as well as a calculator and a handwritten formula sheet.

1.

The 2D unsteady boundary layer equations in Lagrangian coordinates take the form:

u_t = a² u_yy - 2 a b u_xy + b² u_xx + (a a_y - b a_x) u_y + (a b_y - b b_x) u_x

in which a and b can be considered given functions of x and y. Classify this equation. Solution.

2.

Find the rising temperature u(x,t) in a bar with insulated ends if heat is added to the center part of the bar at a constant rate:

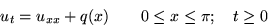
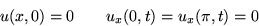
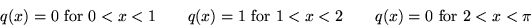
Solution a. Solution b.

3.

Find the unsteady velocity u(y,t) in a fluid that is put into horizontal oscillatory motion by a oscillating shear force. The Navier-Stokes equations for this flow are:

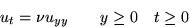
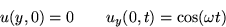
where the frequency of the applied force and the viscosity of the fluid 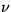are given constants. Solution.

4.

Solve the 3D steady heat conduction inside an infinite circular pipe of radius a if the pipe surface is kept at a constant temperature T₀. Inside the pipe, at a radial distance 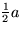away from the axis, there is a point source of heat putting out Q units of heat per unit time.

Using the results, discuss the temperature distribution in cross sections well away from the point heat source. How is the temperature different from T₀? How rapidly does the temperature drop off to T₀ in the axial direction? Solution.