Symmetric Matrices

Definition

A matrix A is symmetric if A^T=A.

Examples:

• mass and stiffness matrices found from the Lagrangian equations;
• finite element methods for structures, fluids, ...;
• inertia matrices of solid bodies;
• ...

Diagonalization:

• Symmetric matrices always have a complete set of independent eigenvectors.
• These eigenvectors are (or at least can be taken to be) orthogonal.

For symmetric matrices, you want to normalize the eigenvectors to length one. In that case, the change of basis to the eigenvectors is simply a rotation of the axis system:

Since the transformation matrix P has orthonormal columns, it is called an orthonormal matrix. For any orthonormal matrix

P^-1 = P^T

Also, both rows and columns will be orthonormal sets of vectors.

Example:

Kinetic energy of a solid body:

where the x,y,z axis system has its origin at the center of gravity.

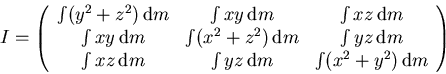
By rotating the x,y,z axis system to the principal axes of the body, the inertia matrix I becomes diagonal.

For a disk:

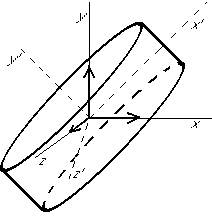
Note that eigenvectors and for this disk are indeterminate, but they are always normal to and you can always take them orthogonal to each other.

10/08/01 0:09:26