Introduction

Eigenvalues:

• buckling;
• modes of vibration;
• dynamical systems;
• principal axes;
• boundary layer instability;
• heat conduction;
• acoustics;
• electrical circuits;
• stability of numerical methods;
• exam questions;
• ...

Definition

A nonzero vector is an eigenvector of a matrix A if is in the same direction as :

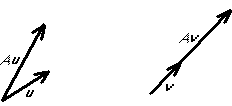
The number is called the corresponding eigenvalue.

An eigenvector is inderminate by a constant that must be chosen.

Example

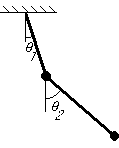
Equations of motion:

Setting

Premultiplying by M^-1 and defining A=M^-1K,

Try solutions of the form

The relative sizes of the components of determine the relative sizes of compared to (the mode shape.)

There will be two different eigenvectors , hence two mode shapes.

Note: we may lose symmetry in the above procedure. There are better ways to do this.

Procedure

Since , so that . For an matrix A, is an n-th degree polynomial in . From it, we can find n eigenvalues ,which do not all need to be distinct.

When these eigenvalues are found, the corresponding eigenvectors follow from solution of .

10/03/01 0:39:28 10/05/01 0:00:10