Complex Matrices

Examples:

• Fourier transforms;
• vibration problems;
• damped wave propagation problems;
• stability of numerical schemes;
• diagonalization;
• ...

Hermitian Conjugate:

The transpose converts rows into columns and vice versa:

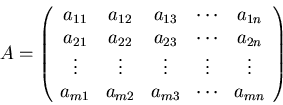
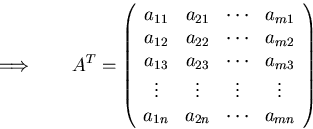
For complex vectors and matrices, you normally want the Hermitian conjugate (or adjoint), which is the complex conjugate transpose:

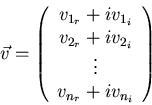
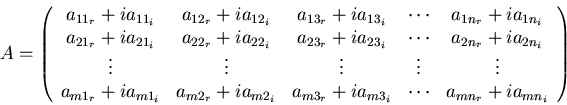
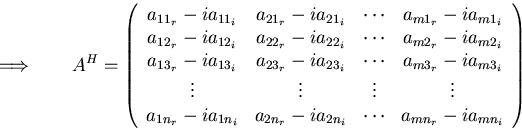
Inner product:

The inner product of two vectors and is:

For real vectors and , this is or equivalently .

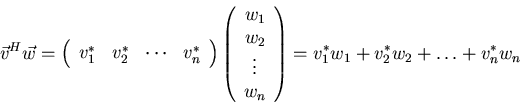
Note however that for complex vectors is not equal to , but its complex conjugate. Order of multiplication matters.

Also note that the book uses a slightly different, less desirable and probably less common, definition.

Norm:

The norm or length of a vector is:

For real vectors , this is ,or equivalently

Orthogonality:

Two vectors and are orthogonal if

For real vectors, that is equivalent to

Unitary Matrices:

A matrix Q is unitary if its columns (or rows) form an orthonormal set. For unitary matrices

Q^-1 = Q^H

10/08/01 0:39:37 10/10/01 0:05:53