Eigenvector Basis

Examples:

• decomposing motion along the fundamental modes;
• writing solid body motion along the principal axes;
• separation of variables;
• improving numerical schemes;
• ...

Diagonalization:

If the matrix A has a complete set of n independent eigenvectors , then A can be diagonalized by using these eigenvectors as a basis S:

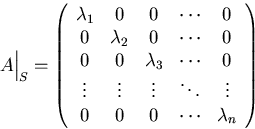
Check:

Note: as long as all n eigenvalues are unequal, there are always n independent eigenvectors.

Matrix transformation rules

For any old basis S and new basis S' with a transformation matrix P, any vector transforms as

Any matrix A transforms as

Check:

One matrix transforms the original, the other matrix transforms the result.

Bottom line

Any matrix A with a complete set of n eigenvectors can be transformed into a simpler, diagonal, matrix and back as

where

• A is the original matrix;
• P is the matrix of eigenvectors (and the transformation matrix)
• is the diagonal matrix with the eigenvalues on the main diagonal.