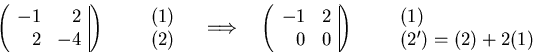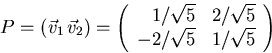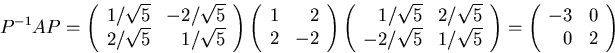Up: 8.66 (a)
Previous: 8.66 (a), §1
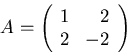
Since AT=A, the matrix is symmetric.
Eigenvalues:

There are two roots: 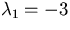 and
and 
The eigenvector corresponding to 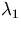 satisfies
satisfies

Taking v1y = -2, then v1x = 1, giving an eigenvector
(1,-2). Normalizing this vector to length one gives:
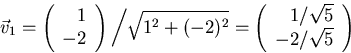
The eigenvector corresponding to 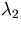 satisfies
satisfies
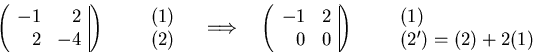
Taking v2y = 1, then v2x = 2, giving after normalization:

Finally:
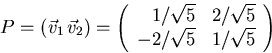
Check:
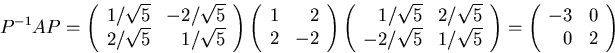
Up: 8.66 (a)
Previous: 8.66 (a), §1
 10/08/01 0:22:19
10/08/01 0:22:19
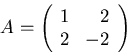
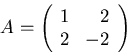

![]() satisfies
satisfies

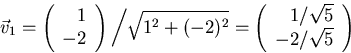
![]() satisfies
satisfies