The below are the simplest possible descriptions of various symbols,
just to help you keep reading if you do not remember/know what they
stand for.
Watch it. There are so many ad hoc usages of symbols, some will have
been overlooked here. Always use common sense first in guessing what
a symbol means in a given context.
-

- A dot might indicate
- A dot product between vectors, if in between them.
- A time derivative of a quantity, if on top of it.
And also many more prosaic things (punctuation signs, decimal points,
...).
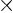
- Multiplication symbol. May indicate:
- An emphatic multiplication.
- Multiplication continued on the next line / from the previous
line.
- A vectorial product between vectors. In index notation,
the
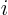 -th component of
-th component of
 equals
equals
where
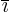 is the index following
is the index following 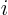 in the sequence
123123..., and
in the sequence
123123..., and
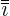 the one preceding it (or second
following). Alternatively, evaluate the determinant
the one preceding it (or second
following). Alternatively, evaluate the determinant
- Might be used to indicate a factorial. Example:
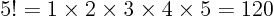 .
.
The function that generalizes 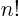 to noninteger values of
to noninteger values of 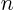 is
called the gamma function;
is
called the gamma function;
 . The gamma function
generalization is due to, who else, Euler. (However, the fact that
. The gamma function
generalization is due to, who else, Euler. (However, the fact that
 instead of
instead of 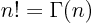 is due to the idiocy of
Legendre.) In Legendre-resistant notation,
is due to the idiocy of
Legendre.) In Legendre-resistant notation,
Straightforward integration shows that 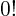 is 1 as it should, and
integration by parts shows that
is 1 as it should, and
integration by parts shows that
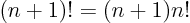 , which ensures that
the integral also produces the correct value of
, which ensures that
the integral also produces the correct value of 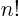 for any higher
integer value of
for any higher
integer value of 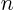 than 0. The integral, however, exists for any
real value of
than 0. The integral, however, exists for any
real value of 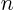 above
above 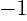 , not just integers. The values of the
integral are always positive, tending to positive infinity for both
, not just integers. The values of the
integral are always positive, tending to positive infinity for both
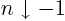 , (because the integral then blows up at small values
of
, (because the integral then blows up at small values
of 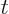 ), and for
), and for
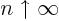 , (because the integral then blows
up at medium-large values of
, (because the integral then blows
up at medium-large values of 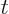 ). In particular, Stirling’s
formula says that for large positive
). In particular, Stirling’s
formula says that for large positive 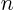 ,
, 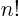 can be approximated
as
can be approximated
as
where the value indicated by the dots becomes negligibly small for
large 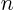 . The function
. The function 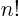 can be extended further to any complex
value of
can be extended further to any complex
value of 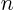 , except the negative integer values of
, except the negative integer values of 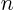 , where
, where 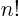 is infinite, but is then no longer positive. Euler’s integral
can be done for
is infinite, but is then no longer positive. Euler’s integral
can be done for 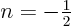 by making the change of variables
by making the change of variables
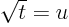 , producing the integral
, producing the integral
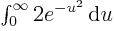 ,
or
,
or
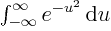 , which equals
, which equals
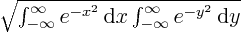 and the integral under the square root can be done analytically
using polar coordinates. The result is that
and the integral under the square root can be done analytically
using polar coordinates. The result is that
To get 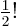 , multiply by
, multiply by  , since
, since  .
.
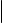
- May indicate:
- The magnitude or absolute value of the number or vector, if
enclosed between a pair of them.
- The determinant of a matrix, if enclosed between a pair of
them.
- The norm of the function, if enclosed between two pairs of them.
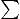
- Summation symbol. Example:
if in three dimensional space a vector
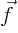 has components
has components
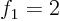 ,
, 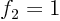 ,
, 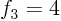 , then
, then
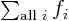 stands for
stands for 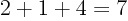 .
.
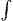
- Integration symbol, the continuous version of the
summation symbol. For example,
is the summation of
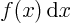 over all little fragments
over all little fragments 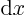 that make up the entire
that make up the entire  -range.
-range.

- May indicate:
- An approaching process.
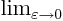 indicates
for practical purposes the value of the expression following the
indicates
for practical purposes the value of the expression following the
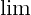 when
when  is extremely small. Similarly,
is extremely small. Similarly,
 indicates the value of the following
expression when
indicates the value of the following
expression when 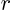 is extremely large.
is extremely large.
- The fact that the left side leads to, or implies, the right-hand
side.
-

- Vector symbol. An arrow above a letter indicates it is a vector. A
vector is a quantity that requires more than one number to be
characterized. Typical vectors in physics include position
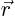 , velocity
, velocity 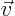 , linear momentum
, linear momentum 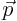 , acceleration
, acceleration 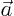 , force
, force 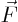 , moment
, moment 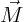 , etcetera.
, etcetera.
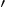
- May indicate:
- A derivative of a function. Examples:
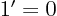 ,
, 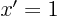 ,
,
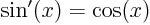 ,
,
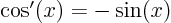 ,
, 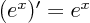 .
.
- A small or modified quantity.

- The spatial differentiation operator nabla. In Cartesian coordinates:
Nabla can be applied to a scalar function 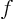 in which case it gives
a vector of partial derivatives called the gradient of the
function:
in which case it gives
a vector of partial derivatives called the gradient of the
function:
Nabla can be applied to a vector in a dot product multiplication, in
which case it gives a scalar function called the divergence of the
vector:
or in index notation
Nabla can also be applied to a vector in a vectorial product
multiplication, in which case it gives a vector function called the curl or rot of the
vector. In index notation, the 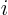 -th component of this vector is
-th component of this vector is
where
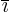 is the index following
is the index following 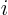 in the sequence 123123...,
and
in the sequence 123123...,
and
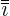 the one preceding it (or the second following it).
the one preceding it (or the second following it).
The operator  is called the Laplacian. In Cartesian coordinates:
is called the Laplacian. In Cartesian coordinates:
In non Cartesian coordinates, don’t guess; look these operators
up in a table book.
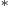
- A superscript star normally
indicates a complex conjugate. In the complex conjugate of a
number, every
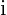 is changed into a
is changed into a 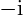 .
.
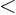
- Less than.
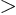
- Greater than.

- Emphatic equals sign.
Typically means “by definition equal” or
“everywhere equal.”
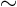
- Indicates approximately equal. Normally the
approximation applies when something is small or large. Read it as
“is approximately equal to.”
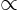
- Proportional to. The two sides are equal except for
some unknown constant factor.

- (Gamma) May indicate:
- The Gamma function. Look under “!” for details.

- (capital delta) May indicate:
- An increment in the quantity following it.
- Often used to indicate the Laplacian
 .
.
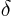
- (delta) May indicate:
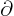
- (partial) Indicates a
vanishingly small change or interval of the following variable. For
example,
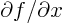 is the ratio of a vanishingly small
change in function
is the ratio of a vanishingly small
change in function 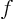 divided by the vanishingly small change in
variable
divided by the vanishingly small change in
variable  that causes this change in
that causes this change in 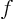 . Such ratios define
derivatives, in this case the partial derivative of
. Such ratios define
derivatives, in this case the partial derivative of 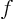 with respect
to
with respect
to  .
.

- (variant of epsilon) May indicate:
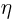
- (eta) May be used to indicate a
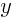 -position.
-position.

- (capital theta) Used in this book
to indicate some function of
 to be determined.
to be determined.

- (theta) May indicate:
- In spherical coordinates, the angle from the chosen
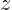 axis, with
apex at the origin.
axis, with
apex at the origin.
- a
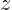 -position.
-position.
- A generic angle, like the one between the vectors in a
cross or dot product.
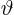
- (variant of theta) An alternate symbol for
 .
.
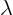
- (lambda) May indicate:
- Wave length.
- An eigenvalue.
- Some multiple of something.
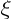
- (xi) May indicate:
- An
 -position.
-position.
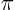
- (pi) May indicate:
- The area of a circle of unit radius. Value 3.141592...
- Half the perimeter of a circle of unit radius. Value 3.141592...
- A 180
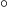 angle expressed in radians. Note that
angle expressed in radians. Note that
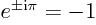 . Value 3.141592...
. Value 3.141592...
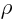
- (rho) May indicate:
- Scaled radial coordinate.
- Radial coordinate.
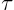
- (tau) May indicate:
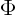
- (capital phi) May indicate:
- Some function of
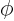 to be determined.
to be determined.
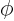
- (phi) May indicate:
- In spherical coordinates, the angle around the chosen
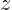 axis. Increasing
axis. Increasing 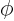 by
by 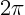 encircles the
encircles the 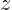 -axis exactly
once.
-axis exactly
once.
- A phase angle.
- Something equivalent to an angle.
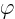
- (variant of phi) May indicate:
- A change in angle
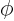 .
.
- An alternate symbol for
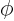 .
.
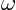
- (omega) May indicate:
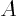
- May indicate:
- Some generic matrix or operator.
- Some constant.
- Area.

- May indicate:
- Acceleration.
- Start point of an integration interval.
- Some coefficient.
- Some constant.
- absolute
- May indicate:
- The absolute value of a real number
 is indicated by
is indicated by  .
It equals
.
It equals  is
is  is positive or zero and
is positive or zero and 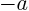 if
if  is negative.
is negative.
- The absolute value of a complex number
 is indicated by
is indicated by
 . It equals the length of the number plotted as a vector in
the complex plane. This simplifies to above definition if
. It equals the length of the number plotted as a vector in
the complex plane. This simplifies to above definition if
 is real.
is real.
- adjoint
- The adjoint
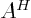 or
or 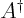 of a matrix is the
complex-conjugate transpose of the matrix.
of a matrix is the
complex-conjugate transpose of the matrix.
Alternatively, it is the matrix you get if you take it to the other
side of an inner product. (While keeping the value of the inner
product the same regardless of whatever two vectors or functions may
be involved.)
“Hermitian”matrices are “self-adjoint;”they are equal to their adjoint. “Skew-Hermitian”matrices are the negative of their adjoint.
“Unitary”matrices are the inverse of their adjoint. Unitary matrices
generalize rotations and reflections of vectors. Unitary operators
preserve inner products.
Fourier transforms are unitary operators on account of the Parseval
equality that says that inner products are preserved.
- angle
- According to trigonometry, if the length of a segment of
a circle is divided by its radius, it gives the total angular extent
of the circle segment. More precisely, it gives the angle, in
radians, between the line from the center to the start of the circle
segment and the line from the center to the end of the segment. The
generalization to three dimensions is called the “solid
angle;” the total solid angle over which a segment of a
spherical surface extends, measured from the center of the sphere,
is the area of that segment divided by the square radius of the
sphere.
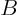
- May indicate:
- A generic second matrix.
- Some constant.
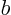
- May indicate:
- End point of an integration interval.
- Some coefficient.
- Some constant.
- basis
- A basis is a minimal set of vectors or functions that you
can write all other vectors or functions in terms of. For example,
the unit vectors
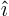 ,
, 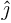 , and
, and 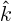 are a basis for
normal three-dimensional space. Every three-dimensional vector can
be written as a linear combination of the three.
are a basis for
normal three-dimensional space. Every three-dimensional vector can
be written as a linear combination of the three.
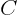
- May indicate:
- A third matrix.
- A constant.
- Cauchy-Schwartz inequality
- The Cauchy-Schwartz inequality describes a limitation on the magnitude
of inner products. In particular, it says that for any vectors
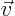 and vec
and vec 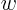
For example, if 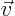 and
and 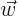 are real vectors, the inner
product is the dot product and we have
are real vectors, the inner
product is the dot product and we have
where  is the length of vector
is the length of vector 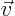 and
and 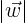 the
one of
the
one of 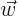 , and
, and  is the angle in between the two
vectors. Since a cosine is less than one in magnitude, the
Cauchy-Schwartz inequality is therefore true for vectors.
is the angle in between the two
vectors. Since a cosine is less than one in magnitude, the
Cauchy-Schwartz inequality is therefore true for vectors.
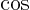
- The cosine function, a periodic function oscillating
between 1 and -1 as shown in [2, pp. 40-...].
- curl
- The curl of a vector field
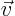 is defined as
is defined as
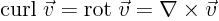 .
.
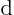
- Indicates a vanishingly small change or interval of the
following variable. For example,
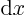 can be thought of as a
small segment of the
can be thought of as a
small segment of the  -axis.
-axis.
- derivative
- A derivative of a function is the ratio of a
vanishingly small change in a function divided by the vanishingly
small change in the independent variable that causes the change in
the function. The derivative of
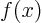 with respect to
with respect to  is
written as
is
written as
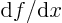 , or also simply as
, or also simply as 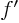 . Note that the
derivative of function
. Note that the
derivative of function 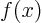 is again a function of
is again a function of  : a ratio
: a ratio
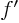 can be found at every point
can be found at every point  . The derivative of a function
. The derivative of a function
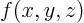 with respect to
with respect to  is written as
is written as
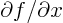 to indicate that there are other
variables,
to indicate that there are other
variables, 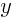 and
and 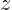 , that do not vary.
, that do not vary.
- determinant
- The determinant of a square matrix
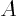 is a single
number indicated by
is a single
number indicated by  . If this number is nonzero,
. If this number is nonzero, 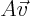 can
be any vector
can
be any vector 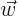 for the right choice of
for the right choice of 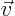 .
Conversely, if the determinant is zero,
.
Conversely, if the determinant is zero, 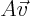 can only produce a
very limited set of vectors. But if it can produce a vector
can only produce a
very limited set of vectors. But if it can produce a vector 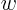 , it
can do so for multiple vectors
, it
can do so for multiple vectors 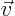 .
.
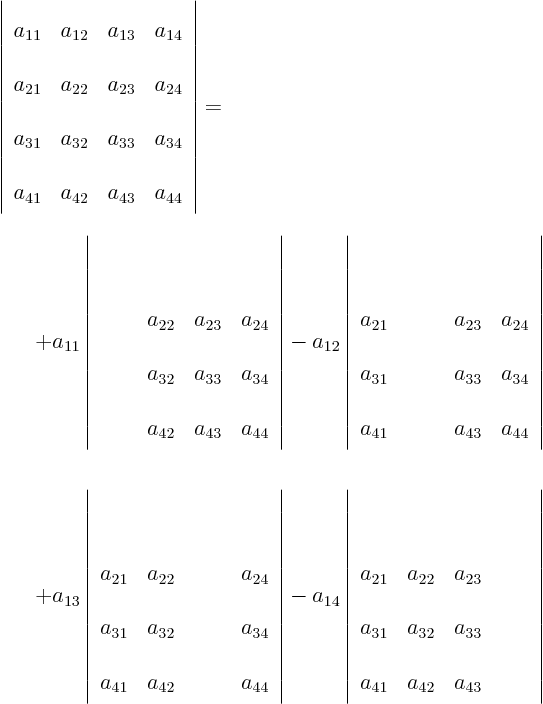
There is a recursive algorithm that allows you to compute
determinants from increasingly bigger matrices in terms of
determinants of smaller matrices. For a 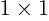 matrix
consisting of a single number, the determinant is simply that
number:
matrix
consisting of a single number, the determinant is simply that
number:
(This determinant should not be confused with the absolute value of
the number, which is written the same way. Since we normally do not
deal with 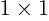 matrices, there is normally no confusion.)
For
matrices, there is normally no confusion.)
For 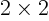 matrices, the determinant can be written in terms of
matrices, the determinant can be written in terms of
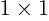 determinants:
determinants:
so the determinant is
 in short.
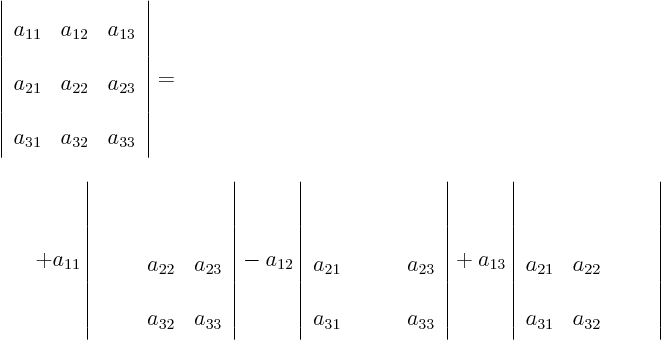
For
in short.
For 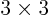 matrices, we have
matrices, we have
and we already know how to work out those 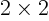 determinants,
so we now know how to do
determinants,
so we now know how to do 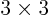 determinants. Written out fully:
determinants. Written out fully:
For 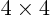 determinants,
determinants,
Etcetera. Note the alternating sign pattern of the terms.
As you might infer from the above, computing a good size determinant
takes a large amount of work. Fortunately, it is possible to
simplify the matrix to put zeros in suitable locations, and that can
cut down the work of finding the determinant greatly. We are
allowed to use the following manipulations without seriously
affecting the computed determinant:
- We may “transpose”the matrix, i.e. change its columns into its rows.
- We can create zeros in a row by subtracting a suitable
multiple of another row.
- We may also swap rows, as long as we remember that each time
that we swap two rows, it will flip over the sign of the computed
determinant.
- We can also multiply an entire row by a constant, but that will
multiply the computed determinant by the same constant.
Applying these tricks in a systematic way, called “Gaussian
elimination” or “reduction to lower triangular
form”, we can eliminate all matrix coefficients 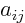 for
which
for
which 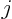 is greater than
is greater than 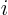 , and that makes evaluating the
determinant pretty much trivial.
, and that makes evaluating the
determinant pretty much trivial.
- div(ergence)
- The divergence of a vector field
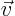 is
defined as
is
defined as
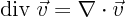 .
.
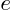
- May indicate:
- The basis for the natural logarithms. Equal to
2.71281828459... This number produces the “exponential
function”
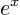 , or
, or 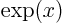 , or in words “
, or in words “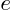 to
the power
to
the power  ”, whose derivative with respect to
”, whose derivative with respect to  is
again
is
again 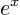 . If
. If  is a constant, then the derivative of
is a constant, then the derivative of
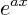 is
is 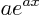 . Also, if
. Also, if  is an ordinary real number,
then
is an ordinary real number,
then 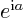 is a complex number with magnitude 1.
is a complex number with magnitude 1.
-

- Assuming
that
 is an ordinary real number, and
is an ordinary real number, and  a real variable,
a real variable,
 is a complex function of magnitude one. The
derivative of
is a complex function of magnitude one. The
derivative of
 with respect to
with respect to  is
is
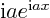
- eigenvector
- A vector
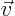 is an eigenvector of a matrix
is an eigenvector of a matrix 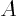 if
if 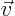 is nonzero and
is nonzero and
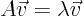 for some number
for some number
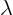 called the corresponding eigenvalue.
called the corresponding eigenvalue.
- exponential function
- A function of the form
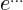 , also
written as
, also
written as 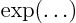 . See function and
. See function and 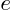 .
.
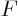
- May indicate:
- The anti-derivative of some function
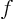 .
.
- Some function.
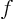
- May indicate:
- A generic function.
- A fraction.
- Frequency.
- function
- A mathematical object that associates values with
other values. A function
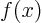 associates every value of
associates every value of  with
a value
with
a value 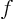 . For example, the function
. For example, the function 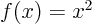 associates
associates 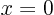 with
with 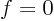 ,
,  with
with 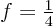 ,
, 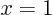 with
with 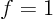 ,
,  with
with 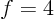 ,
, 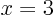 with
with 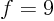 , and more generally, any arbitrary
value of
, and more generally, any arbitrary
value of  with the square of that value
with the square of that value 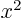 . Similarly,
function
. Similarly,
function 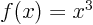 associates any arbitrary
associates any arbitrary  with its cube
with its cube
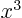 ,
, 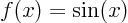 associates any arbitrary
associates any arbitrary  with the sine of
that value, etcetera.
with the sine of
that value, etcetera.
One way of thinking of a function is as a procedure that allows you,
whenever given a number, to compute another number.
- functional
- A functional associates entire functions with single
numbers. For example, the expectation energy is mathematically a
functional: it associates any arbitrary wave function with a number:
the value of the expectation energy if physics is described by that
wave function.
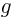
- May indicate:
- A second generic function.
- grad(ient)
- The gradient of a scalar
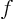 is defined as
is defined as
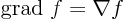 .
.
- The imaginary part of a complex number. If
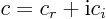 with
with 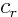 and
and 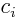 real numbers, then
real numbers, then
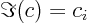 . Note that
. Note that
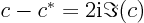 .
.
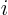
- May indicate:
- The number of a particle.
- A summation index.
- A generic index or counter.
Not to be confused with 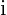 .
.
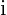
- The standard square root of
minus one:
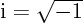 ,
,
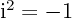 ,
,
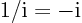 ,
,
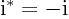 .
.
- index notation
- A more concise and powerful way of writing
vector and matrix components by using a numerical index to indicate
the components. For Cartesian coordinates, we might
number the coordinates
 as 1,
as 1, 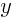 as 2, and
as 2, and 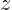 as 3. In that
case, a sum like
as 3. In that
case, a sum like  can be more concisely written as
can be more concisely written as
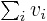 . And a statement like
. And a statement like
 can be
more compactly written as
can be
more compactly written as 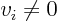 . To really see how it
simplifies the notations, have a look at the matrix entry. (And that
one shows only 2 by 2 matrices. Just imagine 100 by 100 matrices.)
. To really see how it
simplifies the notations, have a look at the matrix entry. (And that
one shows only 2 by 2 matrices. Just imagine 100 by 100 matrices.)
- iff
- Emphatic “if.” Should be read as “if
and only if.”
- integer
- Integer numbers are the whole
numbers:
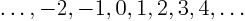 .
.
- inverse
- (Of matrices.) If a matrix
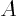 converts a vector
converts a vector 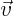 into a vector
into a vector 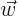 , then the inverse of the matrix,
, then the inverse of the matrix, 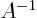 ,
converts
,
converts 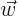 back into
back into 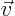 .
.
in other words,
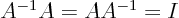 with
with 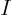 the unit, or
identity, matrix.
the unit, or
identity, matrix.
The inverse of a matrix only exists if the matrix is square and has
nonzero determinant.
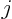
- May indicate:
- A summation index.
- A generic index or counter.
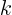
- May indicate:
- A generic summation index.
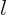
- May indicate:
- The azimuthal quantum number.
- A generic summation index.
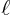
- May indicate:
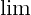
- Indicates the final result of an
approaching process.
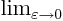 indicates for practical
purposes the value of the following expression when
indicates for practical
purposes the value of the following expression when  is
extremely small.
is
extremely small.
- linear combination
- A very generic concept indicating sums of
objects times coefficients. For example, a position vector
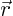 is
the linear combination
is
the linear combination
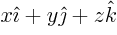 with the objects the
unit vectors
with the objects the
unit vectors 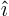 ,
, 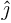 , and
, and 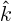 and the coefficients the
position coordinates
and the coefficients the
position coordinates  ,
, 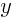 , and
, and 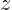 .
.
- matrix
- A table of numbers.
As a simple example, a two-dimensional matrix 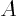 is a table of four
numbers called
is a table of four
numbers called 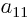 ,
, 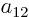 ,
, 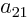 , and
, and  :
:
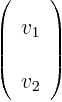
unlike a two-dimensional (ket) vector 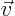 , which would consist of
only two numbers
, which would consist of
only two numbers 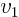 and
and 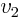 arranged in a column:
arranged in a column:
(Such a vector can be seen as a “rectangular matrix”
of size 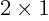 , but let’s not get into that.)
, but let’s not get into that.)
In index notation, a matrix 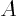 is a set of numbers
is a set of numbers 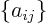 indexed by two indices. The first index
indexed by two indices. The first index 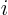 is the row number, the
second index
is the row number, the
second index 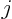 is the column number. A matrix turns a vector
is the column number. A matrix turns a vector 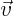 into another vector
into another vector 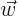 according to the recipe
according to the recipe
where 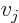 stands for “the
stands for “the 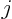 -th component of vector
-th component of vector 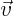 ,” and
,” and  for “the
for “the 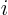 -th component of vector
-th component of vector
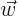 .”
.”
As an example, the product of 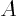 and
and 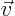 above is by definition
above is by definition
which is another two-dimensional ket vector.
Note that in matrix multiplications like the example above, in
geometric terms we take dot products between the rows of the first
factor and the column of the second factor.
To multiply two matrices together, just think of the columns of the
second matrix as separate vectors. For example:
which is another two-dimensional matrix. In index notation, the 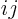 component of the product matrix has value
component of the product matrix has value
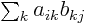 .
.
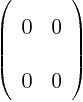
The zero matrix is like the number
zero; it does not change a matrix it is added to and turns
whatever it is multiplied with into zero. A zero matrix is zero
everywhere. In two dimensions:
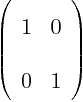
A unit matrix is the equivalent of the
number one for matrices; it does not change the quantity it is
multiplied with. A unit matrix is one on its “main
diagonal” and zero elsewhere. The 2 by 2 unit matrix is:
More generally the coefficients,
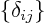 , of a unit matrix
are one if
, of a unit matrix
are one if 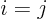 and zero otherwise.
and zero otherwise.
The transpose of a matrix 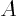 ,
, 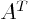 , is what you get if you switch
the two indices. Graphically, it turns its rows into its columns
and vice versa. The Hermitian “adjoint”
, is what you get if you switch
the two indices. Graphically, it turns its rows into its columns
and vice versa. The Hermitian “adjoint”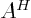 is what you get if you switch the two indices and then take
the complex conjugate of every element. If you want to take a
matrix to the other side of an inner product, you will need to
change it to its Hermitian adjoint. “Hermitian matrices”are equal to their Hermitian adjoint, so this does nothing for them.
is what you get if you switch the two indices and then take
the complex conjugate of every element. If you want to take a
matrix to the other side of an inner product, you will need to
change it to its Hermitian adjoint. “Hermitian matrices”are equal to their Hermitian adjoint, so this does nothing for them.
See also “determinant” and
“eigenvector.”
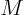
- May indicate:
- Molecular mass. See separate entry.
- Mirror operator.
- Figure of merit.
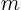
- May indicate:
- Number of rows in a matrix.
- A generic summation index or generic integer.
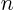
- May indicate:
- Number of columns in a matrix.
- A generic summation index or generic integer.
- A natural number.
and maybe some other stuff.
- natural
- Natural numbers are the numbers:
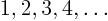 .
.
- normal
- A normal operator or matrix is one that has orthonormal
eigenfunctions or eigenvectors. Since eigenvectors are not
orthonormal in general, a normal operator or matrix is abnormal!
Normal matrices are matrices that commute with their adjoint.
- opposite
- The opposite of a number
 is
is 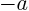 . In other words,
it is the additive inverse.
. In other words,
it is the additive inverse.
- perpendicular bisector
- For two given points
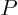 and
and 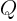 , the
perpendicular bisector consists of all points
, the
perpendicular bisector consists of all points 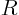 that are equally
far from
that are equally
far from 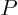 as they are from
as they are from 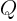 . In two dimensions, the
perpendicular bisector is the line that passes through the point
exactly half way in between
. In two dimensions, the
perpendicular bisector is the line that passes through the point
exactly half way in between 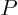 and
and 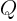 , and that is orthogonal to
the line connecting
, and that is orthogonal to
the line connecting 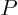 and
and 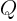 . In three dimensions, the
perpendicular bisector is the plane that passes through the point
exactly half way in between
. In three dimensions, the
perpendicular bisector is the plane that passes through the point
exactly half way in between 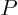 and
and 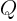 , and that is orthogonal to
the line connecting
, and that is orthogonal to
the line connecting 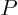 and
and 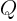 . In vector notation, the
perpendicular bisector of points
. In vector notation, the
perpendicular bisector of points 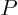 and
and 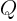 is all points
is all points 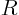 whose
radius vector
whose
radius vector
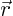 satisfies the equation:
satisfies the equation:
(Note that the halfway point
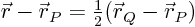 is
included in this formula, as is the half way point plus any vector
that is normal to
is
included in this formula, as is the half way point plus any vector
that is normal to
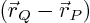 .)
.)
- phase angle
- Any complex number can be written in “polar
form” as
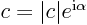 where both the magnitude
where both the magnitude 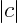 and the phase angle
and the phase angle 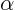 are real numbers. Note that when the
phase angle varies from zero to
are real numbers. Note that when the
phase angle varies from zero to 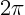 , the complex number
, the complex number 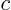 varies from positive real to positive imaginary to negative real to
negative imaginary and back to positive real. When the complex
number is plotted in the complex plane, the phase angle is the
direction of the number relative to the origin. The phase angle
varies from positive real to positive imaginary to negative real to
negative imaginary and back to positive real. When the complex
number is plotted in the complex plane, the phase angle is the
direction of the number relative to the origin. The phase angle
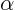 is often called the argument, but so is about everything
else in mathematics, so that is not very helpful.
is often called the argument, but so is about everything
else in mathematics, so that is not very helpful.
In complex time-dependent waves of the form
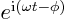 , and its real equivalent
, and its real equivalent
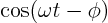 , the phase angle
, the phase angle 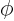 gives the angular
argument of the wave at time zero.
gives the angular
argument of the wave at time zero.
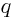
- May indicate:
- Charge.
- Heat flux density.
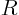
- May indicate:
- Some function of
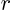 to be determined.
to be determined.
- Some function of
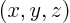 to be determined.
to be determined.
- Some radius.
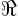
- The real part of a complex number. If
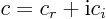 with
with 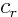 and
and 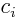 real numbers, then
real numbers, then 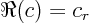 . Note that
. Note that
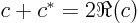 .
.
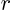
- May indicate:
- The radial distance from the chosen origin of the coordinate
system.
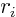 often indicates the
often indicates the 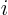 -th Cartesian component of
the radius vector
-th Cartesian component of
the radius vector
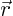 .
.
- Some ratio.
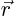
- The position vector. In Cartesian coordinates
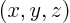 or
or
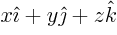 . In spherical coordinates
. In spherical coordinates
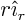 . Its three Cartesian components may be indicated by
. Its three Cartesian components may be indicated by
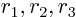 or by
or by 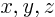 or by
or by 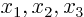 .
.
- reciprocal
- The reciprocal of a number
 is
is 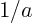 .
In other words, it is the multiplicative inverse.
.
In other words, it is the multiplicative inverse.
- rot
- The rot of a vector
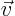 is defined as
is defined as
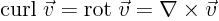 .
.
- scalar
- A quantity characterized by a single number.
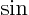
- The sine function, a periodic function oscillating
between 1 and -1 as shown in [2, pp. 40-]. Good to
remember:
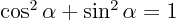 .
.
- Stokes' Theorem
- This theorem, first derived by Kelvin and first
published by someone else I cannot recall, says that for any
reasonably smoothly varying vector
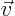 ,
,
where the first integral is over any smooth surface area 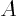 and the
second integral is over the edge of that surface. How did Stokes
get his name on it? He tortured his students with it, that’s
how!
and the
second integral is over the edge of that surface. How did Stokes
get his name on it? He tortured his students with it, that’s
how!
- symmetry
- Symmetries are operations under which an object does
not change. For example, a human face is almost, but not
completely, mirror symmetric: it looks almost the same in a mirror
as when seen directly. The electrical field of a single point
charge is spherically symmetric; it looks the same from whatever
angle you look at it, just like a sphere does. A simple smooth
glass (like a glass of water) is cylindrically symmetric; it looks
the same whatever way you rotate it around its vertical axis.
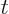
- May indicate:
- triple product
- A product of three vectors. There are two
different versions:
- The scalar triple product
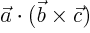 . In index notation,
. In index notation,
where
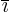 is the index following
is the index following 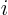 in the sequence
123123..., and
in the sequence
123123..., and
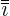 the one preceding it. This triple
product equals the determinant
the one preceding it. This triple
product equals the determinant
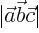 formed
with the three vectors. Geometrically, it is plus or minus the
volume of the parallelepiped that has vectors
formed
with the three vectors. Geometrically, it is plus or minus the
volume of the parallelepiped that has vectors  ,
,
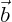 , and
, and 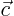 as edges. Either way, as long as the
vectors are normal vectors and not operators,
as edges. Either way, as long as the
vectors are normal vectors and not operators,
and you can change the two sides of the dot product without
changing the triple product, and/or you can change the sides in
the vectorial product with a change of sign.
- The vectorial triple product
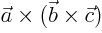 . In index notation,
component number
. In index notation,
component number 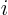 of this triple product is
of this triple product is
which may be rewritten as
In particular, as long as the vectors are normal ones,
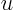
- May indicate:
- The first velocity component in a Cartesian coordinate system.
- An integration variable.
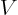
- May indicate:
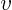
- May indicate:
- The second velocity component in a Cartesian coordinate system.
- Magnitude of a velocity (speed).
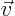
- May indicate:
- Velocity vector.
- Generic vector.
- vector
- A quantity characterized by a list of numbers. A vector
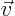 in index notation is a set of numbers
in index notation is a set of numbers 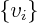 indexed by
an index
indexed by
an index 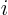 . In normal three-dimensional Cartesian space,
. In normal three-dimensional Cartesian space, 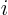 takes the values 1, 2, and 3, making the vector a list of three
numbers,
takes the values 1, 2, and 3, making the vector a list of three
numbers, 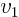 ,
, 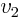 , and
, and 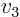 . These numbers are called the
three components of
. These numbers are called the
three components of 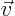 .
.
- vectorial product
- An vectorial product, or cross product is a
product of vectors that produces another vector. If
it means in index notation
that the 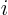 -th component of vector
-th component of vector  is
is
where
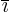 is the index following
is the index following 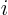 in the sequence 123123...,
and
in the sequence 123123...,
and
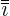 the one preceding it. For example,
the one preceding it. For example, 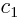 will equal
will equal
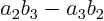 .
.
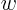
- May indicate:
- The third velocity component in a Cartesian coordinate system.
- Weight factor.
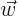
- Generic vector.
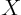
- Used in this book to indicate a function of
 to be
determined.
to be
determined.

- May indicate:
- First coordinate in a Cartesian coordinate system.
- A generic argument of a function.
- An unknown value.
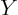
- Used in this book to indicate a
function of
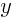 to be determined.
to be determined.
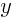
- May indicate:
- Second coordinate in a Cartesian coordinate system.
- A second generic argument of a function.
- A second unknown value.

- Used in this book to indicate a function of
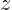 to be
determined.
to be
determined.
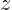
- May indicate:
- Third coordinate in a Cartesian coordinate system.
- A third generic argument of a function.
- A third unknown value.
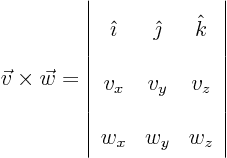
![]() to noninteger values of
to noninteger values of ![]() is
called the gamma function;
is
called the gamma function;
![]() . The gamma function
generalization is due to, who else, Euler. (However, the fact that
. The gamma function
generalization is due to, who else, Euler. (However, the fact that
![]() instead of
instead of ![]() is due to the idiocy of
Legendre.) In Legendre-resistant notation,
is due to the idiocy of
Legendre.) In Legendre-resistant notation,

![]() in which case it gives
a vector of partial derivatives called the gradient of the
function:
in which case it gives
a vector of partial derivatives called the gradient of the
function:

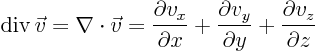
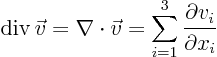
![]() -th component of this vector is
-th component of this vector is
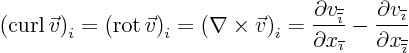
![]() is called the Laplacian. In Cartesian coordinates:
is called the Laplacian. In Cartesian coordinates:
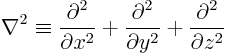
![]() . In two dimensions, take the Laplacian of
. In two dimensions, take the Laplacian of
![]() to get a delta function.
to get a delta function.
![]() matrix
consisting of a single number, the determinant is simply that
number:
matrix
consisting of a single number, the determinant is simply that
number:
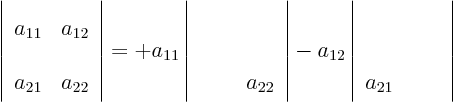
![]() with
with ![]() the unit, or
identity, matrix.
the unit, or
identity, matrix.
![]() is a table of four
numbers called
is a table of four
numbers called ![]() ,
, ![]() ,
, ![]() , and
, and ![]() :
:
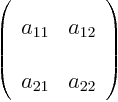
![]() is a set of numbers
is a set of numbers ![]() indexed by two indices. The first index
indexed by two indices. The first index ![]() is the row number, the
second index
is the row number, the
second index ![]() is the column number. A matrix turns a vector
is the column number. A matrix turns a vector ![]() into another vector
into another vector ![]() according to the recipe
according to the recipe
![]() and
and ![]() above is by definition
above is by definition
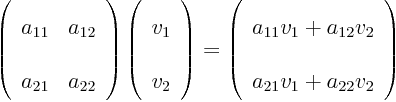
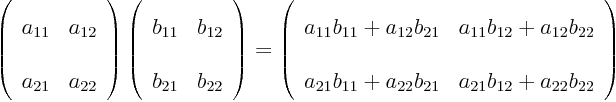
![]() ,
, ![]() , is what you get if you switch
the two indices. Graphically, it turns its rows into its columns
and vice versa. The Hermitian “adjoint”
, is what you get if you switch
the two indices. Graphically, it turns its rows into its columns
and vice versa. The Hermitian “adjoint”![]() is what you get if you switch the two indices and then take
the complex conjugate of every element. If you want to take a
matrix to the other side of an inner product, you will need to
change it to its Hermitian adjoint. “Hermitian matrices”are equal to their Hermitian adjoint, so this does nothing for them.
is what you get if you switch the two indices and then take
the complex conjugate of every element. If you want to take a
matrix to the other side of an inner product, you will need to
change it to its Hermitian adjoint. “Hermitian matrices”are equal to their Hermitian adjoint, so this does nothing for them.
![]() , and its real equivalent
, and its real equivalent
![]() , the phase angle
, the phase angle ![]() gives the angular
argument of the wave at time zero.
gives the angular
argument of the wave at time zero.